Hola buenas, por lo que usamos en el ejercicio 1 de este mismo practico para demostrar que los vaps son reales. No debería haber un circulo simétrico con respeto al eje real, a otro que uno contenga lamda y otro lamda conjugado?
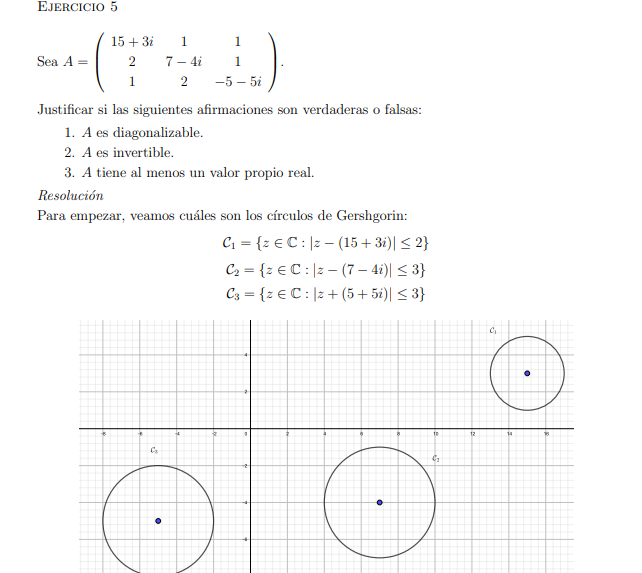
Hola buenas, por lo que usamos en el ejercicio 1 de este mismo practico para demostrar que los vaps son reales. No debería haber un circulo simétrico con respeto al eje real, a otro que uno contenga lamda y otro lamda conjugado?

 será un polinomio con
coeficientes reales.
será un polinomio con
coeficientes reales.