hola, tengo dudas sobre esta función: si tomamos Ω= C - {0}, como Ω tiene agujero entonces la integral de 1/z en una curva cerrada alrededor de Ω no puede ser 0, y esa función no tiene primitiva, no puede ser holomorfa. Entonces, para que la integral de 1/z alrededor de una curva cerrada sea cero, debe ser holomorfa en Ω, y además Ω debe ser simplemente conexa en la zona de la curva cerrada. O sea, la curva no puede contener agujeros. Entonces en este ejercicio que encontré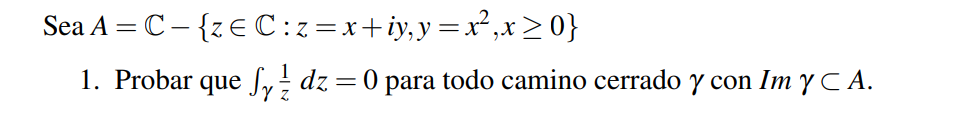
me preguntaba cómo podía ser 0 la integral, ya que A contiene agujero en 0 (cuando x=0, y=0 entonces). Se me ha ocurrido que el camino cerrado justo no encierre los agujeros que tenga A , pero no me doy cuenta qué camino cerrado podía ser