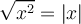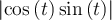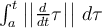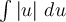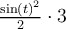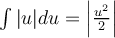El ejercicio 7)b) plantea que la solución es 6. Sin embargo el ejercicio 5 contiene la misma curva, y el largo da menor a 6... ¿cómo es posible? (aclaro que no pude resolver la integral de "raíz de (sen^4(x) + (cos^4(x))" pero igual quisiera saber su resultado)
Hola. La curva del ejercicio 7b no es la misma que la del ejercicio 5. Sólo coinciden en un pedacito, fijate los dominios de la parametrización.
Por otro lado, revisá con atención las cuentas ya que no te deberia quedar esa expresión.
Un abrazo
Me sumo a la duda, la exprecion que a la que llego para integrar es
3 [cos^4(t)sen^2(t) + sen^4(t)cos^2(t)]^1/2 y usando la equivalencia
sen^2 +cos^2 = 1 llego a 3 sen(t)cos(t) con t en [0,2pi] . cuando hago la integral me da cero.
ahi sacas factor comun sen^2cos^2 y te queda (sen^2cos^2(sen^2+cos^2))1/2= sen*cos
lo que pasa es que 
, entonces el integrando es siempre positivo y no se anula.
tenes que integrar el valor absoluto: 3
Buenas, tengo 2 dudas:
La definición de longitud de arco es,
No debería dejarse planteado así y que vaya hasta t? Haciendolo hasta el intervalo que dice el ejercicio me da bien la parte (a), pero seria la longitud propiamente dicha.
En la parte b, dejando el 3 de lado:
Haciendo el cambio de variable sen(t) = u, queda
Lo que sería: 
Deshaciendo el cambio quedaría:
Entre 0 y 2pi, lo que me da 0.
Creo que estoy haciendo mal la integral con el valor absoluto, pero vos dijiste que siempre es positivo el integrando, por lo que sacaría las barras no?
Saludos!
te cuento como lo pense yo, viste la intergral esta :
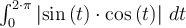
agarre y la dividi en 4:
1 - va de 0 a pi/2
2 - va de pi/2 a pi
3 - va de pi a 3pi/2
4 - va de 3pi/2 a 2pi
a esto lo hice porque dependiendo de cuanto sea el angulo es el signo de seno y coseno, de ese modo podes sacar las barras, porejemplo para la primera te qeda integral de sen*cos, ya que seno y coseno son los dos positivos si el angulo es entre 0 y pi/2, despues la segunda te qeda integral de sen*-cos esto ya que el seno es positivo y el coseno negativos para esos valores, despues sumas todos los resultados y da, no se si esta bien, pero parese rasonable y da, saludos
Está perfecto.
es falso. Deriva la expresión de la derecha para verlo.
Perfecto, me quedó claro! gracias a ambos.
Saludos!
Es un viaje este ejercicio. Tenes que saber de antemano muchas reglas trigonometricas.
El modulo de la traza me dio 3.cos(t).sin(t), y la integral no la hice entre 0 y 2pi, sino que la hice entre 0 y pi/2, y luego la multiplique por 4, ya que sino no sale.