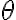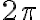Buenas, pude llegar a que la expresión de la velocidad angular, y encontré el ángulo para el cual la velocidad se anula, pero no se me ocurre cómo demostrar que la masa se mantiene en reposo en esa posición. Gracias.
Otra cosa, para la parte c, llegué a la misma expresión que indica la solución:
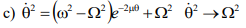
Si esta expresión fuera en función del tiempo, es evidente que la velocidad límite es la indicada, pero me queda la duda de que, si en realidad, la velocidad no oscila, ya que theta toma valores de 0 a 2pi.
Buen día Pablo.
Efectivamente, esa ecuación para la velocidad depende del tiempo.
Efectivamente, esa ecuación para la velocidad depende del tiempo.
El ángulo 
es una función dependiente 
.
es una función dependiente .Fijate que la función que contiene a 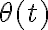en su argumento es una exponencial negativa (no una exponencial compleja, como sería en el caso de una función oscilante). 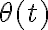se mide en radiantes y crece con t, lo que hace que la exponencial decrezca y, por ende, la velocidad también.
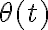en su argumento es una exponencial negativa (no una exponencial compleja, como sería en el caso de una función oscilante). 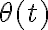se mide en radiantes y crece con t, lo que hace que la exponencial decrezca y, por ende, la velocidad también. Observa que los mayores a 
simplemente nos indican que la masa ha dado más de una vuelta.
mayores a simplemente nos indican que la masa ha dado más de una vuelta.Saludos!
Lo que pasa que en el momento que la velocidad se haga cero la fuerza neta también lo es
En cuanto a qué Tita vale hasta 2Pi me parece que sigue creciendo en cada vuelta
En cuanto a qué Tita vale hasta 2Pi me parece que sigue creciendo en cada vuelta