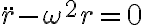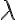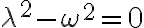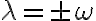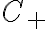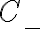No me quedo claro en las soluciones porque al prinicipio define la solucion de r como c por e a la landa.t y despues lo hace como una suma de dos exponenciales. No me deja subir la foto pero es en la mitad de la página 3 de las soluciones.
Me parece que hay un error al definir landa porque dice que es igual a omega. t y de la ecuacion de la que despeja obtenes que landa = omega. Desde ya muchas gracias.
Saludos, Michele.
Hola Michele,
la ecuación de movimiento
admite una exponencial 
como solución mientras 
satisfaga el polinomio característico de la misma:
,
cuyas raíces son en este caso 
(como bien nos hacés notar, se coló un 
de más al escribir esa parte de la solución, lo corregiremos en breve). Como se trata de dos raíces diferentes, la exponencial con una raiz es linealmente independiente de la exponencial con la otra, por lo que la solución más general a la ecuación diferencial corresponde a la combinación lineal de las exponenciales:
(la ecuación diferencial es lineal y homogénea, por lo que si admite cada solución por separado admite también la combinación de ellas).
Las constantes 
y 
se ajustan luego de acuerdo a las condiciones iniciales, tal como está indicado más adelante en la página 3.
Sii, esa era mi duda. Muchas gracias!!
Buenas, me quedé con la duda en este ejercicio de como darse cuenta que el sistema movil planteado en la solución, solidario al tubo (O, er, eφ, k) es un sistema no inercial. Yo lo que había entendido es que para que el sistema sea no inercial tiene que estar acelerado con respecto al sistema fijo. Mi pregunta es que basta con que rote con respecto al sistema fijo para que sea no inercial, en este caso con velocidad angular constante w?
De la 2a ley de Newton se puede demostrar que solo los sistemas que se trasladan con velocidad constante respecto a un sistema inercial, son inerciales. Por lo tanto los sistemas que rotan con velocidad angular no son inerciales (porque no se trasladan, sino que rotan). Y eso se puede ver en el caso del ejercicio porque la aceleración de arrastre o transporte y la de Coriolis son no nulas. En particular la aceleración de arrastre o transporte tiene una componente centrípeta. Así que un sistema que gira con velocidad angular constante respecto a un sistema inercial introduce una aceleración centrípeta. O sea que está acelerado y no es inercial.