Buenas, no sabría bien como arrancarlo este ejercicio.
Plantea la fuerza neta tangencial o sea según etita. Para resolver preintegra multiplicando por Tita punto
Para N trabaja con la fuerza neta radial después de llegar a la expresión de Tita punto al cuadrado
Para N trabaja con la fuerza neta radial después de llegar a la expresión de Tita punto al cuadrado
Hola! ¿Qué sistema de coordenadas conviene usar? yo lo planteé con intrínsecas pero me queda la aceleración tangencial igualada a g×cos(tita) y no sabría como resolver la ecuación (ni si descompuse correctamente el peso). Muchas gracias!
Hola Lucía,
lo más conveniente es trabajar en coordenadas polares.
Por otro lado, no podría decirte cómo resolver la ecuación sin ver a qué llegaste.
Te pido si podés subir una foto de tu desarrollo para verificar si es correcto y sugerirte cómo continuar.
Saludos!
lo más conveniente es trabajar en coordenadas polares.
Por otro lado, no podría decirte cómo resolver la ecuación sin ver a qué llegaste.
Te pido si podés subir una foto de tu desarrollo para verificar si es correcto y sugerirte cómo continuar.
Saludos!
Buenas! Lo planteé con coordenadas polares cilíndricas pero estaría llegando a un resultado diferente a la solución, no logro ver mi error, me vendría bien una ayuda, muchas gracias.
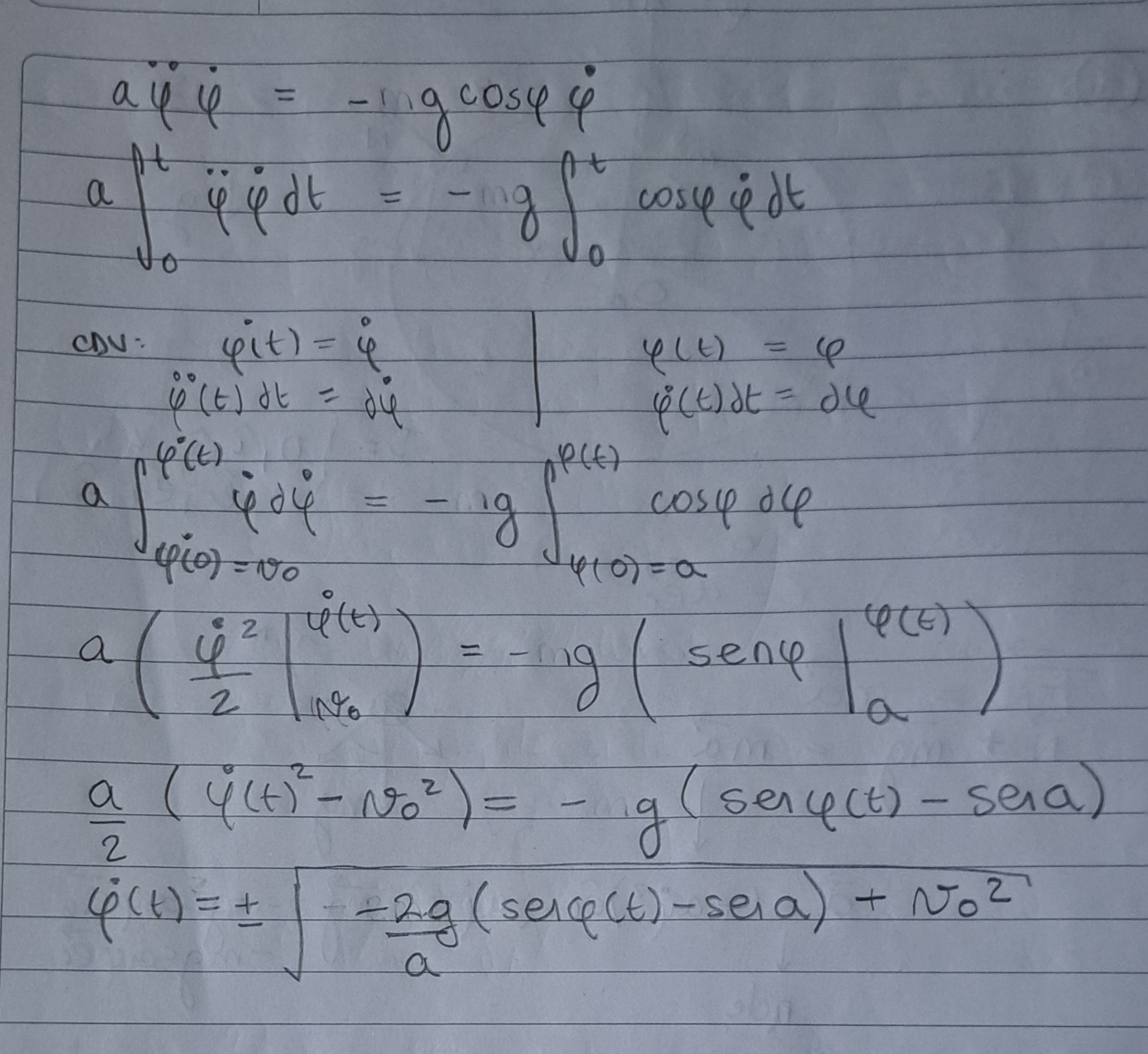
Hola, Lucía.
Primero que nada, tené cuidado con los errores dimensionales.
Primero que nada, tené cuidado con los errores dimensionales.
- Uno de ellos es al plantear Newton según 
(aunque todavía no lo necesitás)
(aunque todavía no lo necesitás)- otros dos en las condiciones iniciales: al imponer 
, cuando son cantidades dimensionalmente diferentes.
, cuando son cantidades dimensionalmente diferentes.- y al imponer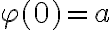 
(un ángulo no puede ser igual a una distancia)
Lo que mencionás de la diferencia entre la ecuación de movimiento que vos encontrás y la de la solución, es que la de la solución utiliza una cordenada
que es la complementaria al 
que vos usas. Esto implica cambios en el signo del versor tangencial, en las expresiones de senos y cosenos, etc.
Siquerés chequear tu resultado con la solución, una vez que termines el ejercicio, podes hacer el cambio de variable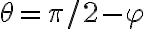
y verificar que todo de igual. Otra opción, por su puesto, es que uses la misma coordenada para hacer el ejercicio desde el inicio, pero no está mal que vos te definas la coordenada que tengas ganas.
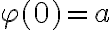(un ángulo no puede ser igual a una distancia)Lo que mencionás de la diferencia entre la ecuación de movimiento que vos encontrás y la de la solución, es que la de la solución utiliza una cordenada
que es la complementaria al que vos usas. Esto implica cambios en el signo del versor tangencial, en las expresiones de senos y cosenos, etc. Siquerés chequear tu resultado con la solución, una vez que termines el ejercicio, podes hacer el cambio de variable
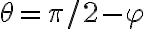y verificar que todo de igual. Otra opción, por su puesto, es que uses la misma coordenada para hacer el ejercicio desde el inicio, pero no está mal que vos te definas la coordenada que tengas ganas.Cualquier cosa repreguntá.
Saludos