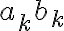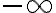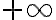Lo que pasa es que la exponencial compleja
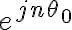
, con
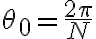
es periódica de periodo
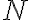
por lo que para calcular los coeficientes de Fourier en el caso discreto solo hay que sumar sobre un periodo, ya que luego tanto los valores de
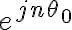
como de
![x[n] x[n]](https://eva.fing.edu.uy/filter/tex/pix.php/d3baaa3204e2a03ef9528a7d631a4806.gif)
se vuelven a repetir; lo mismo pasa con la base
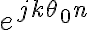
, por lo que la síntesis de la señal
![x[n] x[n]](https://eva.fing.edu.uy/filter/tex/pix.php/d3baaa3204e2a03ef9528a7d631a4806.gif)
no se escribe descompuesta sobre una base infinita, sino que sobre una finita, en un periodo.
Me parece que hay un error en la letra y debería decir " .... son los coeficientes de Fourier de
![x[n] x[n]](https://eva.fing.edu.uy/filter/tex/pix.php/d3baaa3204e2a03ef9528a7d631a4806.gif)
,
![y[n] y[n]](https://eva.fing.edu.uy/filter/tex/pix.php/a39037ba03412351ec1f3c8ca9e807fd.gif)
y
![z[n] z[n]](https://eva.fing.edu.uy/filter/tex/pix.php/8a8c996b9e9d1294c8f815911479257f.gif)
... "
Vos tenes que
![a_k = \frac{1}{N} \sum_{n=\prec N\succ}x[n]e^{-jk\theta_{0}n} a_k = \frac{1}{N} \sum_{n=\prec N\succ}x[n]e^{-jk\theta_{0}n}](https://eva.fing.edu.uy/filter/tex/pix.php/8c4a1e54f234b0fe43071f6ffa3cf696.gif)
,
![b_k = \frac{1}{N} \sum_{n=\prec N\succ}y[n]e^{-jk\theta_{0}n} b_k = \frac{1}{N} \sum_{n=\prec N\succ}y[n]e^{-jk\theta_{0}n}](https://eva.fing.edu.uy/filter/tex/pix.php/8289ec81ea75e2a511d38e65b365dbcf.gif)
,
![c_k = \frac{1}{N} \sum_{n=\prec N\succ}\sum_{r=\prec N\succ}x[r]y[n-r]e^{-jk\theta_{0}n} c_k = \frac{1}{N} \sum_{n=\prec N\succ}\sum_{r=\prec N\succ}x[r]y[n-r]e^{-jk\theta_{0}n}](https://eva.fing.edu.uy/filter/tex/pix.php/51665def1be72fffe25982f871c38e35.gif)
.
Ahora
![a_k b_k = \frac{1}{N^2} (\sum_{n=\prec N\succ}x[n]e^{-jk\theta_{0}n})( \sum_{n=\prec N\succ}y[n]e^{-jk\theta_{0}n}) a_k b_k = \frac{1}{N^2} (\sum_{n=\prec N\succ}x[n]e^{-jk\theta_{0}n})( \sum_{n=\prec N\succ}y[n]e^{-jk\theta_{0}n})](https://eva.fing.edu.uy/filter/tex/pix.php/648dcbd6cecc2d06cf3f638dd6d02a0b.gif)
. Pensando como quedaría lo anterior si agrupas lo que multiplica a cada
![x[r] x[r]](https://eva.fing.edu.uy/filter/tex/pix.php/28f23a0192c4b16ad197077511552170.gif)
y sumando sobre cada
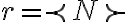
![a_k b_k = \frac{1}{N^2} \sum_{r=\prec N\succ}(x[r]e^{-jk\theta_{0}r} \sum_{n=\prec N\succ}y[n-r]e^{-jk\theta_{0}(n-r)}) a_k b_k = \frac{1}{N^2} \sum_{r=\prec N\succ}(x[r]e^{-jk\theta_{0}r} \sum_{n=\prec N\succ}y[n-r]e^{-jk\theta_{0}(n-r)})](https://eva.fing.edu.uy/filter/tex/pix.php/9690346416318ee538f250ab83cb9bb1.gif)
Acá no tenes problema con
![y[n] y[n]](https://eva.fing.edu.uy/filter/tex/pix.php/a39037ba03412351ec1f3c8ca9e807fd.gif)
ni con
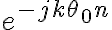
porque como son periódicas de periodo
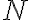
el que las corras r no afecta a la igualdad. Como
![x[r]e^{-jk\theta_{0}r} x[r]e^{-jk\theta_{0}r}](https://eva.fing.edu.uy/filter/tex/pix.php/7b428433f5cdc87d9b15ee1dcd27588a.gif)
no depende de

,lo podes meter dentro de la segunda sumatoria y te queda
![a_k b_k = \frac{1}{N^2}\sum_{r=\prec N\succ}\sum_{n=\prec N\succ}x[r]e^{-jk\theta_{0}r}y[n-r]e^{-jk\theta_{0}(n-r)} = \frac{1}{N^2}\sum_{r=\prec N\succ}\sum_{n=\prec N\succ}x[r]y[n-r]e^{-jk\theta_{0}n} a_k b_k = \frac{1}{N^2}\sum_{r=\prec N\succ}\sum_{n=\prec N\succ}x[r]e^{-jk\theta_{0}r}y[n-r]e^{-jk\theta_{0}(n-r)} = \frac{1}{N^2}\sum_{r=\prec N\succ}\sum_{n=\prec N\succ}x[r]y[n-r]e^{-jk\theta_{0}n}](https://eva.fing.edu.uy/filter/tex/pix.php/dc4257d0aa0e721e5c9b12d74dc78d23.gif)
.
Finalmente intercambiando las sumatorias
![a_k b_k = \frac{1}{N^2}\sum_{n=\prec N\succ}\sum_{r=\prec N\succ}x[r]y[n-r]e^{-jk\theta_{0}n} = \frac{c_k}{N} a_k b_k = \frac{1}{N^2}\sum_{n=\prec N\succ}\sum_{r=\prec N\succ}x[r]y[n-r]e^{-jk\theta_{0}n} = \frac{c_k}{N}](https://eva.fing.edu.uy/filter/tex/pix.php/35fb04fe4ac09ff629dbcf5dc37b674e.gif)
La propiedad de las series de Fourier de la convolución periódica es exactamente lo que demostrás en este ejercicio.
Si hay algún error, les agradezco me lo hagan saber.
Espero se entienda bien, un saludo.

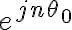
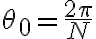
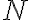
![x[n] x[n]](https://eva.fing.edu.uy/filter/tex/pix.php/d3baaa3204e2a03ef9528a7d631a4806.gif)
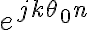
![y[n] y[n]](https://eva.fing.edu.uy/filter/tex/pix.php/a39037ba03412351ec1f3c8ca9e807fd.gif)
![z[n] z[n]](https://eva.fing.edu.uy/filter/tex/pix.php/8a8c996b9e9d1294c8f815911479257f.gif)
![a_k = \frac{1}{N} \sum_{n=\prec N\succ}x[n]e^{-jk\theta_{0}n} a_k = \frac{1}{N} \sum_{n=\prec N\succ}x[n]e^{-jk\theta_{0}n}](https://eva.fing.edu.uy/filter/tex/pix.php/8c4a1e54f234b0fe43071f6ffa3cf696.gif)
![b_k = \frac{1}{N} \sum_{n=\prec N\succ}y[n]e^{-jk\theta_{0}n} b_k = \frac{1}{N} \sum_{n=\prec N\succ}y[n]e^{-jk\theta_{0}n}](https://eva.fing.edu.uy/filter/tex/pix.php/8289ec81ea75e2a511d38e65b365dbcf.gif)
![c_k = \frac{1}{N} \sum_{n=\prec N\succ}\sum_{r=\prec N\succ}x[r]y[n-r]e^{-jk\theta_{0}n} c_k = \frac{1}{N} \sum_{n=\prec N\succ}\sum_{r=\prec N\succ}x[r]y[n-r]e^{-jk\theta_{0}n}](https://eva.fing.edu.uy/filter/tex/pix.php/51665def1be72fffe25982f871c38e35.gif)
![a_k b_k = \frac{1}{N^2} (\sum_{n=\prec N\succ}x[n]e^{-jk\theta_{0}n})( \sum_{n=\prec N\succ}y[n]e^{-jk\theta_{0}n}) a_k b_k = \frac{1}{N^2} (\sum_{n=\prec N\succ}x[n]e^{-jk\theta_{0}n})( \sum_{n=\prec N\succ}y[n]e^{-jk\theta_{0}n})](https://eva.fing.edu.uy/filter/tex/pix.php/648dcbd6cecc2d06cf3f638dd6d02a0b.gif)
![x[r] x[r]](https://eva.fing.edu.uy/filter/tex/pix.php/28f23a0192c4b16ad197077511552170.gif)
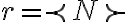
![a_k b_k = \frac{1}{N^2} \sum_{r=\prec N\succ}(x[r]e^{-jk\theta_{0}r} \sum_{n=\prec N\succ}y[n-r]e^{-jk\theta_{0}(n-r)}) a_k b_k = \frac{1}{N^2} \sum_{r=\prec N\succ}(x[r]e^{-jk\theta_{0}r} \sum_{n=\prec N\succ}y[n-r]e^{-jk\theta_{0}(n-r)})](https://eva.fing.edu.uy/filter/tex/pix.php/9690346416318ee538f250ab83cb9bb1.gif)
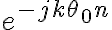
![x[r]e^{-jk\theta_{0}r} x[r]e^{-jk\theta_{0}r}](https://eva.fing.edu.uy/filter/tex/pix.php/7b428433f5cdc87d9b15ee1dcd27588a.gif)

![a_k b_k = \frac{1}{N^2}\sum_{r=\prec N\succ}\sum_{n=\prec N\succ}x[r]e^{-jk\theta_{0}r}y[n-r]e^{-jk\theta_{0}(n-r)} = \frac{1}{N^2}\sum_{r=\prec N\succ}\sum_{n=\prec N\succ}x[r]y[n-r]e^{-jk\theta_{0}n} a_k b_k = \frac{1}{N^2}\sum_{r=\prec N\succ}\sum_{n=\prec N\succ}x[r]e^{-jk\theta_{0}r}y[n-r]e^{-jk\theta_{0}(n-r)} = \frac{1}{N^2}\sum_{r=\prec N\succ}\sum_{n=\prec N\succ}x[r]y[n-r]e^{-jk\theta_{0}n}](https://eva.fing.edu.uy/filter/tex/pix.php/dc4257d0aa0e721e5c9b12d74dc78d23.gif)
![a_k b_k = \frac{1}{N^2}\sum_{n=\prec N\succ}\sum_{r=\prec N\succ}x[r]y[n-r]e^{-jk\theta_{0}n} = \frac{c_k}{N} a_k b_k = \frac{1}{N^2}\sum_{n=\prec N\succ}\sum_{r=\prec N\succ}x[r]y[n-r]e^{-jk\theta_{0}n} = \frac{c_k}{N}](https://eva.fing.edu.uy/filter/tex/pix.php/35fb04fe4ac09ff629dbcf5dc37b674e.gif)
![y[n] = y[n-r] y[n] = y[n-r]](https://eva.fing.edu.uy/filter/tex/pix.php/e50135ad8cc60a3fb6377f1fe34f71e5.gif)