Foro de dudas del práctico 2

Hola.

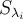La idea es que se apoyen en la parte anterior. Una de las formas de ver que una suma de subespacios es directa y que da todo $V$, es ver que si tomamos una base de cada subespacio $S_{\lambda_i}$ y las unimos, obtenemos una base de $V$. Como los 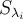$S_{\lambda_i}$ son subespacios propios asociados a valores propios distintos, sabemos que si tomamos una base de cada subespacio y las unimos, eso da un conjunto linealmente independiente, por lo que tan solo hay que ver que genera $V$ para que la suma directa dé $V$.

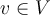Teniendo en cuenta lo anterior, lo que falta hacer para ver que $S_{\lambda_1} \oplus S_{\lambda_2} \oplus S_{\lambda_3} = V$, es ver que cualquier vector de $v\in V$ puede escribirse como la suma de tres vectores 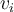$v_i$, cada uno en 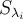$S_{\lambda_i}$ (esto es equivalente a que el conjunto linealmente independiente que mencionamos antes, obtenido de unir las bases de 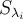$S_{\lambda_i}$, sea generador de $V$ ).

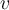Ahora, dado un vector $v$, la parte anterior del ejercicio te da una forma de obtener tres vectores, cada uno en un 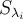$S_{\lambda_i}$, a partir de 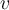$v$. La sugerencia es que trates de escribir a 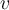$v$ combinando esos tres vectores de alguna forma. Probá si con eso se te ocurre. Cualquier cosa podés volver a consultar por acá.

Saludos!