ejercicio 11 practico 2

ejercicio 11 practico 2

de Matias Daniel Alvarez Silva -
Número de respuestas: 7

Buenos dias. los valores propios de puede que sean Lamda1= 1+a (raiz doble), lamda2=2a, lmda3=-2a  ??. porque no estoy pudiendo resolver el ej y quiza tenga los valores propios mal. Gacias. 

En respuesta a Matias Daniel Alvarez Silva

Re: ejercicio 11 practico 2

de Roberto Elbio Peroni Martinez -
A mí me dieron 1+a triple y 1-a
En respuesta a Roberto Elbio Peroni Martinez

Re: ejercicio 11 practico 2

de Matias Daniel Alvarez Silva -

Asi quedo la matriz asociada usando la base canonica.

En respuesta a Matias Daniel Alvarez Silva

Re: ejercicio 11 practico 2

de Roberto Elbio Peroni Martinez -
No se te simplifica el dos del numerador con el del denominador.
(1-x)^2-a^2=0 entonces
(1-x)^2=a^2
1-x =+ - a
En respuesta a Roberto Elbio Peroni Martinez

Re: ejercicio 11 practico 2

de Tabare Nahuel Roland Silveira -
Hola.
Las raíces son 1+a, que es triple, y 1-a, que es simple. Según como le quedo a Matías el polinomio característico, para factorizar (1-\lambda)^2 - a^2, despejando como dijo Roberto queda 1-\lambda = \pm a, y despejando \lambda queda \lambda = 1 \pm a.
Con esas raíces pueden continuar el ejercicio.
Saludos!
En respuesta a Tabare Nahuel Roland Silveira

Re: ejercicio 11 practico 2

de Matias Daniel Alvarez Silva -
Puede ser que T sea diagonalizable para todo valor de A ?
En respuesta a Matias Daniel Alvarez Silva

Re: ejercicio 11 practico 2

de Roberto Elbio Peroni Martinez -

Llegué a la misma conclusión 

En respuesta a Roberto Elbio Peroni Martinez

Re: ejercicio 11 practico 2

de Tabare Nahuel Roland Silveira -
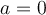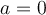Sí, da eso. Un comentario respecto a lo anterior, si a vale cero, como 1+a=1-a, en este caso particular hay un único valor propio, que es raíz cuádruple del polinomio característico. Si se fijan, de todas formas también quedará diagonalizable, porque si a=0 la transformación lineal es simplemente la identidad.
Saludos!