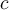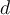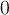FVC-1S: 4.b

Queria tener una idea de como encarar este ejercicio. Lo que pense fue buscar 3 puntos pertenecientes a una recta generica, y restringir la recta para que la imagen por la transformacion fuese tambien una recta. Como la ecuacion de una recta generica que pasa por el origen es y=ax, entonces T(x+yi)= T(x+xai)=(2x+2axi-i)/(-ix+ax-2)

Y tome otros dos puntos como imagen de la transformacion T(0)=i/2 y T(infinito) = 2i

El problema es que no se como restringir la transformacion de la recta generica para que tambien el resultado este en el eje imaginario y T vaya a una recta

Re: 4.b

de Marcos Martinez Leiranes - miércoles, 22 de marzo de 2023, 18:56

Hola,

Te tiro una idea un poco más geométrica. Fijate lo siguiente, considerate una möbius

$T(z)=\frac{az+b}{cz+d}$ con

$c$ y

$d$ no nulos. En ese caso, toda recta (aunque también vale para cfa) se va a convertir en una recta si y solo si en algún punto de la recta se cumple que

$T(z)=\infty$ . Tenes muchas formas de ver eso, la que me sirve a mi de forma intuitiva es imaginando que una recta si le agrego el infinito como que forma una especie de circunferencia. Ahora volviendo al ejercicio, vos sabes que una recta queda definida por dos puntos, al

$0$ ya lo fijaste por lo que basta tomar la recta que pasa por

$0$ y el

$z$ que cumple que

$T(z)=\infty$ . Como sabes que solo hay una recta que pasa por esos dos puntos entonces ya terminaste el ejercicio.

Lo probé en un caso general, pero poniendo números lo podes adaptar al ejercicio. Cualquier cosa si no quedó claro volvé a escribir o lo hablamos después de alguna de las clases, si es que asistis alguna.

Saludos.