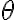Buenas, en el ejemplo que da de una partícula en el interior de un aro llega a una expresión que se tiene que cumplir para que la bola llegue desde A hasta B. Pero lo que no entiendo es qué condición impone para que eso se cumpla, parece que se cumpliera por sí solo.
Entiendo que ![\dot{\theta}\geq 0,\forall\theta\in[0,\pi]](https://eva.fing.edu.uy/filter/tex/pix.php/3f9793448e60591cd97544ddcfbaaa8b.png "\dot{\theta}\geq 0,\forall\theta\in[0,\pi]")
pero no es necesario imponer dicha condición ya que lo del lado derecho de esta ecuación
debería de ser siempre positivo sin importar el signo de tita punto ya que está elevado al cuadrado.
Entonces, si la condición para llegar a B se da por sí sola, significa que ese llega a B siempre?
Gracias
