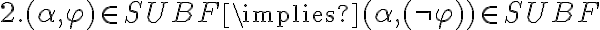Buenas,
No consigo definir el conjunto de forma inductivo, no termino de entender en cual de las dos entradas debo ir aplicando las regla para definirlo.
Ejemplo:
Sé que 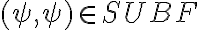 .
.
Pero no sé si debo dar las reglas como: 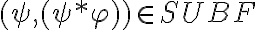
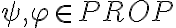 .
.
O si la segunda entrada no se modifica, solo debo dar las reglas para la primera entrada en base a la formula que está en la segunda entrada. No sé si me explico... Lo pensaría como: si tengo 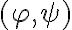 tengo que dar
tengo que dar  en funcion de
en funcion de 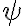 .
.
Igualmente, no estoy viendo la forma de inducir todo el conjunto de esta manera.. Si me pudieran ayudar, les agradecería.
Saludos!