Hola, todo bien? en el video de presentación del práctico se habla de demostrar un lema para seguir con la demostración... no entendí que lema sería, cuál sería?
Desde ya gracias
Hola, todo bien? en el video de presentación del práctico se habla de demostrar un lema para seguir con la demostración... no entendí que lema sería, cuál sería?
Desde ya gracias
Hola José:
A partir del minuto 46 del video, está la explicación del lema del cuál se habla.
Sería algo así:
Lema:
H)
- s es una secuencia de formación
- s' es un prefijo de s
T) s' es una secuencia de formación
Si quedan dudas, volvé a preguntar.
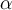 ): Sea
): Sea  secuencia de formacion para
secuencia de formacion para 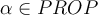 ->
->  secuencia de formacion de
secuencia de formacion de 
 es atomico entonces se cumple la propiedad ya que si tengo una secuencia de formacion que termina en un atomico entonces es secuencia para esa proposicion atomica.
es atomico entonces se cumple la propiedad ya que si tengo una secuencia de formacion que termina en un atomico entonces es secuencia para esa proposicion atomica.