Foro práctico 4

Buenas quería hacer una consulta sobre este ejercicio.

Tenemos lo composición del logaritmo con la función $\phi = \frac{z+1}{1-z}$ la cual es un trasformación de Moebius. Sabemos que el logaritmo complejo de la rama principal no es continuo en la semirrecta $R^{+}\cup \lbrace 0 \rbrace$   

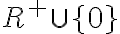
Entonces tendríamos que la composición no puede ser derivable en los puntos 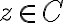$z \in C$ tales que si imagen por 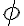$\phi$ vaya a parar a esa semirrecta donde no es continuo, ni tampoco derivable, el logaritmo. Esto es correcto?

Tenemos que $\phi = \frac{z+1}{1-z}$ y se observa que 

• $\phi(-1) = 0$ 
• $\phi(0) = 1$ 
• $\phi(1) = \infty$ 

Entonces podemos ver que si tomamos 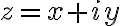$z= x+iy$ entonces 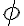$\phi$ manda al conjunto 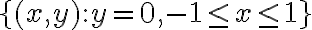$\lbrace (x,y): y=0, -1 \leq x \leq 1 \rbrace$ en la semirrecta.

La composición no podría ser derivable en esos puntos, no? Quiero decir respondiendo a la pregunta del ejercicio $Log \circ \phi$ es derivable en $C - \lbrace (x,y): y=0, -1 \leq x \leq 1 \rbrace$

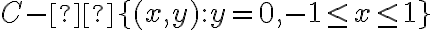
Saludos.