Buenas, tengo una consulta respecto a la parte b del ejercicio y es que no logro darme cuenta de porque en la solucion toman que T(a)=0 y T(b)=infinito.

Buenas, tengo una consulta respecto a la parte b del ejercicio y es que no logro darme cuenta de porque en la solucion toman que T(a)=0 y T(b)=infinito.

 que lleve el segmento
que lleve el segmento ![[a.b] [a.b]](https://eva.fing.edu.uy/filter/tex/pix.php/0c75f6114ded252a092a353dcd386aac.gif) en
en 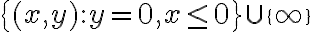 . Si uno consigue una transformación de Mobius asi, entonces como es biyectiva, el complemento de
. Si uno consigue una transformación de Mobius asi, entonces como es biyectiva, el complemento de ![[a.b] [a.b]](https://eva.fing.edu.uy/filter/tex/pix.php/0c75f6114ded252a092a353dcd386aac.gif) va en el complemento de
va en el complemento de 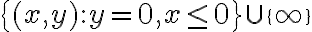 , en otras palabras, manda
, en otras palabras, manda ![\mathbb{C} - [a,b] \mathbb{C} - [a,b]](https://eva.fing.edu.uy/filter/tex/pix.php/05f55203132d727a8b9b0c9cb638f4fe.gif) en
en 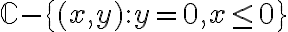 , que es lo deseado.
, que es lo deseado.![[a,b] [a,b]](https://eva.fing.edu.uy/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) en
en 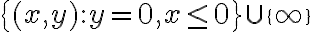 hay varias opciones, pero lo que si o si debe ocurrir es que
hay varias opciones, pero lo que si o si debe ocurrir es que  ,
, 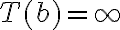 o
o 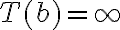 y
y 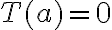 . Te convence eso?
. Te convence eso?![[a,b] [a,b]](https://eva.fing.edu.uy/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) vaya en el eje real.
vaya en el eje real.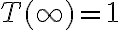 . Creo que aca hay algo importante que entender, voy a ver si lo explico bien:
. Creo que aca hay algo importante que entender, voy a ver si lo explico bien: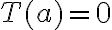 ,
, 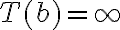
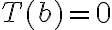 ,
, 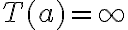 .
.![[a.b] [a.b]](https://eva.fing.edu.uy/filter/tex/pix.php/0c75f6114ded252a092a353dcd386aac.gif) debe ir a todo el eje real (con el infinito claro).
debe ir a todo el eje real (con el infinito claro).![[a,b] [a,b]](https://eva.fing.edu.uy/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) va en el eje real pero en principio podría ser que
va en el eje real pero en principio podría ser que ![[a.b] [a.b]](https://eva.fing.edu.uy/filter/tex/pix.php/0c75f6114ded252a092a353dcd386aac.gif) vaya a
vaya a 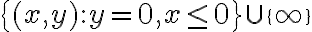 , o a la otra parte del eje real
, o a la otra parte del eje real 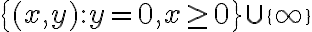 . Entonces estas condiciones ( 1) + 2), o 1) + 3)), no alcanzan.
. Entonces estas condiciones ( 1) + 2), o 1) + 3)), no alcanzan.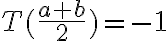 : esto alcanza, porque mandé tres puntos del segmento
: esto alcanza, porque mandé tres puntos del segmento ![[a.b] [a.b]](https://eva.fing.edu.uy/filter/tex/pix.php/0c75f6114ded252a092a353dcd386aac.gif) en tres puntos del segmento real, entonces si o si la transformación de Mobius me manda el segmente
en tres puntos del segmento real, entonces si o si la transformación de Mobius me manda el segmente ![[a,b] [a,b]](https://eva.fing.edu.uy/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) en un segmento del eje real. Como
en un segmento del eje real. Como 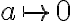 ;
; 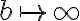 y el punto medio de
y el punto medio de ![[a,b] [a,b]](https://eva.fing.edu.uy/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) va en
va en 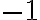 , entonces no queda otra que
, entonces no queda otra que ![T([a,b]) = \{ (x,y): y=0, x \leq 0 \} \cup \{\infty\} T([a,b]) = \{ (x,y): y=0, x \leq 0 \} \cup \{\infty\}](https://eva.fing.edu.uy/filter/tex/pix.php/8132cd1b3a287546964d7589e5c4145b.gif) .
.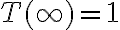 : veamos por qué esta opción alcanza. Es claro que
: veamos por qué esta opción alcanza. Es claro que ![T([a,b]) T([a,b])](https://eva.fing.edu.uy/filter/tex/pix.php/5b29f4c72ae3dfa39a5bb68b29aa4b8e.gif) va a parar a un segmento del eje real cuyo borde son los puntos
va a parar a un segmento del eje real cuyo borde son los puntos 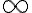 y
y  . Hay dos segmentos del eje real que cumplen esto. Aca eje real siempre es junto con el infinito. Si le llamo
. Hay dos segmentos del eje real que cumplen esto. Aca eje real siempre es junto con el infinito. Si le llamo  a la recta que contiene a
a la recta que contiene a ![[a.b] [a.b]](https://eva.fing.edu.uy/filter/tex/pix.php/0c75f6114ded252a092a353dcd386aac.gif) , lo que sucede es que
, lo que sucede es que ![[a,b] [a,b]](https://eva.fing.edu.uy/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) va para un segmento del eje real, y
va para un segmento del eje real, y ![r - [a,b] r - [a,b]](https://eva.fing.edu.uy/filter/tex/pix.php/a0ca09452eed5a8ac49cce964c140504.gif) va para el otro. Como
va para el otro. Como ![\infty \in r-[a.b] \infty \in r-[a.b]](https://eva.fing.edu.uy/filter/tex/pix.php/d4d31dfd24679a7e9459d727974823e9.gif) y
y 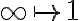 es claro que
es claro que ![r-[a,b] r-[a,b]](https://eva.fing.edu.uy/filter/tex/pix.php/ad1d8d56b1ca37b72d74630469cf9d55.gif) va para el segmento
va para el segmento 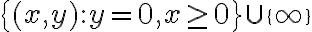 , entonces
, entonces ![[a.b] [a.b]](https://eva.fing.edu.uy/filter/tex/pix.php/0c75f6114ded252a092a353dcd386aac.gif) va para el otro, como era deseado.
va para el otro, como era deseado.  termina dando
termina dando 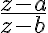 mientras que la opción B esta dando
mientras que la opción B esta dando 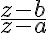 (revisar, hice las cuentas acá en un papel).
(revisar, hice las cuentas acá en un papel). del segmento
del segmento ![[a,b] [a,b]](https://eva.fing.edu.uy/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) hasta el punto
hasta el punto  entonces en la opción A) estoy recorriendo desde
entonces en la opción A) estoy recorriendo desde  hasta
hasta 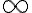 caminando por los reales negativos. La opción
caminando por los reales negativos. La opción 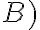 hace lo contrario, camina para el otro lado, si por los reales negativos, pero partiendo desde
hace lo contrario, camina para el otro lado, si por los reales negativos, pero partiendo desde 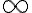 hasta
hasta  .
. vaya para los negativos, que además es lo que pide la letra.
vaya para los negativos, que además es lo que pide la letra.