Hola, te contesté en persona pero contesto por acá en caso que alguien más se haya trancado con eso.
Supongamos que es par, entonces se cumple la siguiente igualdad:
es par, entonces se cumple la siguiente igualdad: 
Si pasamos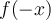 restando entonces tenemos que
restando entonces tenemos que  . En otras palabras llegamos a que la serie de potencia de los impares nos da la función nula, por lo que concluímos que
. En otras palabras llegamos a que la serie de potencia de los impares nos da la función nula, por lo que concluímos que  para todo
para todo 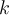 . El caso en que la función es impar es análogo.
. El caso en que la función es impar es análogo.
Saludos!
Supongamos que
 es par, entonces se cumple la siguiente igualdad:
es par, entonces se cumple la siguiente igualdad: 
Si pasamos
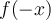 restando entonces tenemos que
restando entonces tenemos que  . En otras palabras llegamos a que la serie de potencia de los impares nos da la función nula, por lo que concluímos que
. En otras palabras llegamos a que la serie de potencia de los impares nos da la función nula, por lo que concluímos que  para todo
para todo 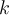 . El caso en que la función es impar es análogo.
. El caso en que la función es impar es análogo.Saludos!