Ejemplo:
Σ = {a,b}
Σ* = Σ
Si w ∈ S, wa ∈ S
La primer línea parece ser la definición del alfabeto.
La segunda línea, no la entiendo.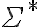 
es un conjunto muy específico, dado 
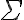y no entiendo cómo podría ser igual a .
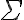La tercer línea sí la entiendo creo que allí está la pregunta :-) .
La tercer línea parece ser una regla de definición de un conjunto. Consideremos un conjunto que tiene esta regla como única regla en su definición.
La pregunta que nos tenemos que hacer siempre es:
- Cuál es el mínimo conjunto que cumple con la definición del conjunto?
Para ver esto, consideremos lo siguiente, en algún momento arbitrario de la construcción del conjunto:
- Tengo algún elemento
en S para agregarle una 'a' atrás y construir un nuevo elemento?
- Como no tengo elementos en S (aún) no puedo construir un nuevo elemento para agregarlo al conjunto.
Conclusión: El conjunto que se construye es el conjunto vacío.
El conjunto vacío, cumple con estar definición inductiva?
- SI. Si lo vemos desde el punto de vista lógico, la regla tiene la estructura
- Si <CONDICION 1> entonces <CONDICION 2>
- Como la <CONDICION 1> no se cumple (o sea, es falsa) entonces, sin importar si la <CONDICION 2> si la <CONDICION 2> se cumple, la regla (el total de la regla) se cumple.
Eso no pasa si tenemos reglas base, por en algún momento de la construcción del conjunto tengo para elegir un elemento (proporcionado por las reglas base) y construir un elemento nuevo para agregar en el conjunto.
De esta forma: Si no hay reglas base, el conjunto que se define es el vacío.