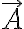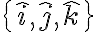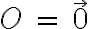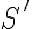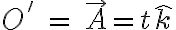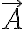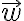Hola, tengo una duda respecto a la ecuación (1.35) de las notas que dice 
¿Qué pasa si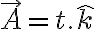 
y S' es un sistema de referencia paralelo a S = {i,j,k} con origen en A?
¿
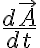no me tendría que dar 
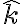y sin embargo con la ecuación me daría el vector nulo? Porque como el origen de S' está en A, para los ojos de S', A es el vector nulo por lo que 
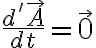y también 
porque S' no rota con respecto a S.
Gracias.
89 palabras
que es la posición del origen de S' respecto a S. en S no es el vector nulo en S', sino que tiene distintas componentes en uno u otro sistema, como indican las ecuaciones (1.25) y (1.26).97 palabras
Entendí todo, solo que no veo la diferencia. Para el ejemplo que di, ¿cómo sería? Digamos. 
con versores 
y origen 
y 
con versores y origen 
. ¿Cómo quedaría 
en las coordenadas de ? ¿Y el vector 
de la ecuación 1.35?
Saludos!
48 palabras
, escritas sus componentes en dos sistemas de referencia distintos, pero es el mismo vector.67 palabras
Ahí va. Lo que no me daba cuenta es que para un vector cualquiera lo único que importa es su módulo, dirección y sentido; no importa su punto de origen. Entonces tanto da poner al vector A con origen en O como con origen en O', el vector sigue siendo el mismo (aunque lo haya trasladado), por lo que para el sistema S', por más de que esté trasladándose, como tiene mismos versores que S, A se escribe igual para S y para S'. O sea, en el ejemplo A=t.k también para S', y bueno, el vector w igual al vector nulo.
Saludos!
103 palabras