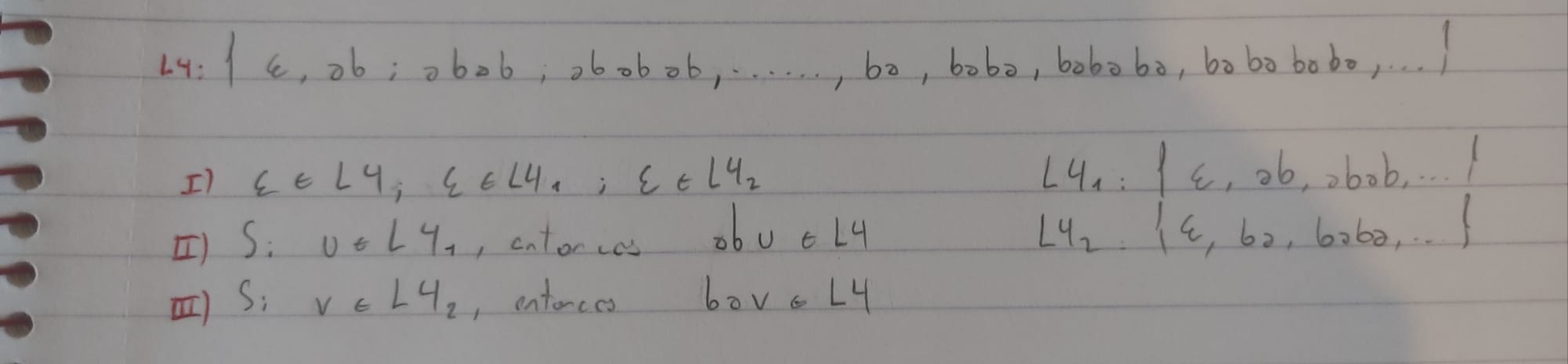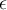Ejercicio 8: duda respecto a L4 y L5

Ejercicio 8: duda respecto a L4 y L5

de Jose Agustin Bizio Piriz -
Número de respuestas: 9

Hola muy buenas, tenia una duda muy puntual sobre como definir ambos conjuntos, mi idea es usar un condicional, es decir, definirlo de forma similar a esto:

\epsilon \in L_4

a \in L_4

b \in L_4

Si w termina en a -> wb \in L_4

Si w termina en b -> wa \in L_4

No se me estaría ocurriendo otra manera que no sea usando estos condicionales (diciendo que w termine en a/b), pero no tengo entendido del todo si se puede usar ya que estaría dadole "estructura" a w, cosa que no se puede hacer.

Si tienen otra solución con la que me puedan ayudar estaría bueno que la digan o al menos una pista.

Desde ya gracias, Agustín.
En respuesta a Jose Agustin Bizio Piriz

Re: Ejercicio 8: duda respecto a L4 y L5

de Guillermo Calderon - InCo -

Buenas:

En este curso no aceptamos definiciones inductivas con ese tipo de reglas:

si w termina en "a" entonces ...
si w termina en "b" entonces ...

Estas pueden dar lugar a definiciones incorrectas o que no cumplen con las propiedades de una definición inductiva simple.

Para definir L4 se sugiere definir dos lenguajes auxiliares:

  • L4₁ - Tiras de la forma: abab⋯ab
  • L4₂ - Tiras de la forma: baba⋯ba

Luego se da una definición inductiva de L4 a partir de los dos conjuntos anteriores.

Para definir L5 te sugiero que tengas en cuenta que L5 está formado por 2 tipos de tiras:

  • abab ... ab - Repeticiones de ab.
  • abab ... aba - Las tiras anteriores (repeticiones de ab) con una a al final.
En respuesta a Guillermo Calderon - InCo

Re: Ejercicio 8: duda respecto a L4 y L5

de Martin Jose Bula Sire -
¿Sería válida la siguiente definición de L4?
Dada la función copiar : Σ*×N → Σ* tal que
(i) copiar(u, 0) = ε ∀u ∈ Σ*;
(ii) copiar(u, n+1) = ucopiar(u, n) ∀u ∈ Σ*, ∀n ∈ N
se define el lenguaje L4 ⊂ {a, b}* por
(i) ε ∈ L4;
(ii) ab ∈ L4;
(iii) ba ∈ L4;
(iv) u ∈ L4 ⇒ copiar(u, n) ∈ L4 ∀n ∈ N.
En respuesta a Martin Jose Bula Sire

Re: Ejercicio 8: duda respecto a L4 y L5

de Guillermo Calderon - InCo -

Hola Martín:

En principio te comento que tu solución es un poco extraña porque se basa en definir una función particular que es la que se encarga de generar (casi) todas las tiras.

Normalmente cuando uno da una definición inductiva, la propia definición nos provee un método para generar las tiras:

  • arrancamos con los elementos dados por las claúsulas base y aplicamos un número finito de veces las cláusulas inductivas.

De esta manera se generan todas las tiras del conjunto.

En tu definición, cada tira se genera por aplicación de la función copia. En realidad, hay una cláusula inductiva pero que no es necesaria. Una definición más breve usando tu misma técnica sería:

  • Si n \in \mathbf{N} entonces \text{copia(ba,n)} \in L_4
  • Si n \in \mathbf{N^+} entonces \text{copia(ab,n)} \in L_4

y no necesitamos claúsula inductiva porque de esta manera se generan todas las tiras del conjunto.

También podemos osbservar que la definición que vos das no es libre porque podés generar de muchas formas distintas la misma tira: abababab = copia(ab,4) + copia(abab,2).

Estrictamente hablando, no puedo decir que la definición sea incorrecta. La solución es algo rara porque usa una función auxiliar y porque da lugar a una definición que podemos llamar degenerada ya que no tiene claúsulas inductivas.

De todos modos, la definición está muy original y dentro de todo funciona.
En respuesta a Guillermo Calderon - InCo

Re: Ejercicio 8: duda respecto a L4 y L5

de Diego Ismael Marichal Chavez -
Hola, siguiendo la idea para L4, seria asi como quedaria resuelto? 
Tambien tengo una duda, que pasa si mis reglas permite definir mas elementos de los que tiene L4, estaria correcto para lo que pide el ejercicio?
Saludos
Diego

En respuesta a Diego Ismael Marichal Chavez

Re: Ejercicio 8: duda respecto a L4 y L5

de Guillermo Calderon - InCo -

La idea es un poco diferente. Lo que sugerimos es definir cada conjunto de manera independiente. Son 3 definiciones distintas:

  1. Definición de L4-1 = {\epsilon, ab, abab, ababab, ....., }
  2. Definición de L4'2 = {\epsilon, ba, baba, bababa, ....., }
  3. Definición de L4 como la unión de los dos lenguajes anteriores

Las definiciones de L4-1 y L4-2 son completamente independientes. La definición de L4 usa a los dos lenguajes anteriores.

Con respecto a:

¿qué pasa si mis reglas permite definir mas elementos de los que tiene L4, estaria correcto para lo que pide el ejercicio?

No, no estaría correcto. Estaría definiendo un super conjunto del conjunto pedido.
En respuesta a Guillermo Calderon - InCo

Re: Ejercicio 8: duda respecto a L4 y L5

de Diego Ismael Marichal Chavez -
Hola, gracias por la respuesta, entonces quedaria asi, o me falta algo respecto a L4?

En respuesta a Diego Ismael Marichal Chavez

Re: Ejercicio 8: duda respecto a L4 y L5

de Guillermo Calderon - InCo -

Bueno, casi estaría.

Un par de detalles:

  • Tenés que dar una definición inductiva de L4. Entonces tenés que escribir algo equivalente a decir que L4 es la unión de los otros dos pero que sea una definición inductiva. Esto es, con cláusualas base e inductivas.

  • La tira nula está en L41 y L42; eso te va generar algún problema cuando escribas la únión de ambos. (te queda una definición no libre). Pero es muy fácil de arreglar.

En respuesta a Guillermo Calderon - InCo

Re: Ejercicio 8: duda respecto a L4 y L5

de Joaquín Sande González -
¿Es válido usar como condición para una regla, el que un elemento pertenezca a otro conjunto?

Se me había ocurrido la siguiente solución, pero no sé si es correcta debido a que no sé si las reglas inductivas son correctas:

Debo definir L4: {ε, ab, abab, ababab, abababab, . . . , ba, baba, bababa, babababa, . . .}

Para eso defino L4₁ como:
I) ε ∈ L4₁
II) si ɑ ∈ L4₁ ⇒ ɑab ∈ L4₁
(es decir que L4₁ = {ε, ab, abab, ababab, ...})

y luego defino L4₂ como:
I) ε ∈ L4₂
II) si ɑ ∈ L4₂ ⇒ ɑba ∈ L4₂
(es decir que L4₂ = {ε, ba, baba, bababa, ...})

y por último defino a L4 como:
I) ε ∈ L4
II) si ɑ ∈ L4₁ ⇒ ɑab ∈ L4
II) si ɑ ∈ L4₂ ⇒ ɑba ∈ L4

(y ahí está mi duda. ¿Es válido usar "si alfa pertenece a L4₁", o "alfa pertenece a L4₂" como una condición para aplicarle la regla?)
Gracias.