Hola, no entiendo la partición que hacen del p, porque yo planteo que
(√3/2)r<z<r entonces en el pasaje a esféricas queda (√3/2)r/cos alfa<p< r/cos alfa
Hola, no entiendo la partición que hacen del p, porque yo planteo que
(√3/2)r<z<r entonces en el pasaje a esféricas queda (√3/2)r/cos alfa<p< r/cos alfa
Hola. Ojo que  se va a mover entre
se va a mover entre 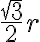 y el techo dado por la esfera (que es
y el techo dado por la esfera (que es  si
si 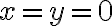 , pero no es igual a
, pero no es igual a  si
si  y
y  no son 0. Mi consejo es que, en lugar de usar esféricas, uses cilíndricas: podés pensar que
no son 0. Mi consejo es que, en lugar de usar esféricas, uses cilíndricas: podés pensar que  e
e  se mueven en la circunferencia que surge de cortar la esfera con el plano
se mueven en la circunferencia que surge de cortar la esfera con el plano 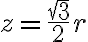 (esa circunferencia tiene ecuación
(esa circunferencia tiene ecuación 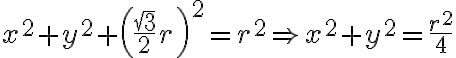 ) y que
) y que  va de
va de 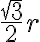 a la esfera (que, traducida a cilíndricas, tiene ecuación
a la esfera (que, traducida a cilíndricas, tiene ecuación 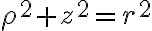 ).
).
Saludos