Buenas, en la parte c del primer ejercicio no entiendo la solución, no me doy cuenta de como ver la espira y la bobina como un circuito eléctrico y no entiendo como considera la inclinación de la segunda. ¿Alguien me lo podría explicar?
Gracias.
Buenas, en la parte c del primer ejercicio no entiendo la solución, no me doy cuenta de como ver la espira y la bobina como un circuito eléctrico y no entiendo como considera la inclinación de la segunda. ¿Alguien me lo podría explicar?
Gracias.
 en el eje) y una bobina pequeña que se pone sobre el eje z, pero no se coloca colineal a este sino que se la rota un ángulo
en el eje) y una bobina pequeña que se pone sobre el eje z, pero no se coloca colineal a este sino que se la rota un ángulo 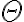 . En la figura del ejercicio se observan tres rayitas y el ángulo
. En la figura del ejercicio se observan tres rayitas y el ángulo 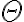 , los cuales representan la bobina. Como se considera el tamaño de la bobina como muy pequeño, entonces del flujo magnético que pasa a través de ella es el generado por el
, los cuales representan la bobina. Como se considera el tamaño de la bobina como muy pequeño, entonces del flujo magnético que pasa a través de ella es el generado por el 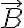 hallado sobre el eje en la parte a). De esta forma calcula el flujo magnético como
hallado sobre el eje en la parte a). De esta forma calcula el flujo magnético como 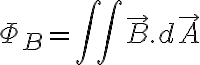 , como hay un producto escalar entre el vector campo magnético y el vector diferencial área, de ahí aparece el término
, como hay un producto escalar entre el vector campo magnético y el vector diferencial área, de ahí aparece el término 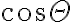 .
. .
.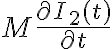 y la resistencia
y la resistencia 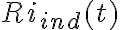 , donde
, donde 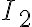 es la corriente que circula por la bobina e
es la corriente que circula por la bobina e 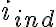 es la corriente que circula por la espira grande.
es la corriente que circula por la espira grande.Buenas Lucia,
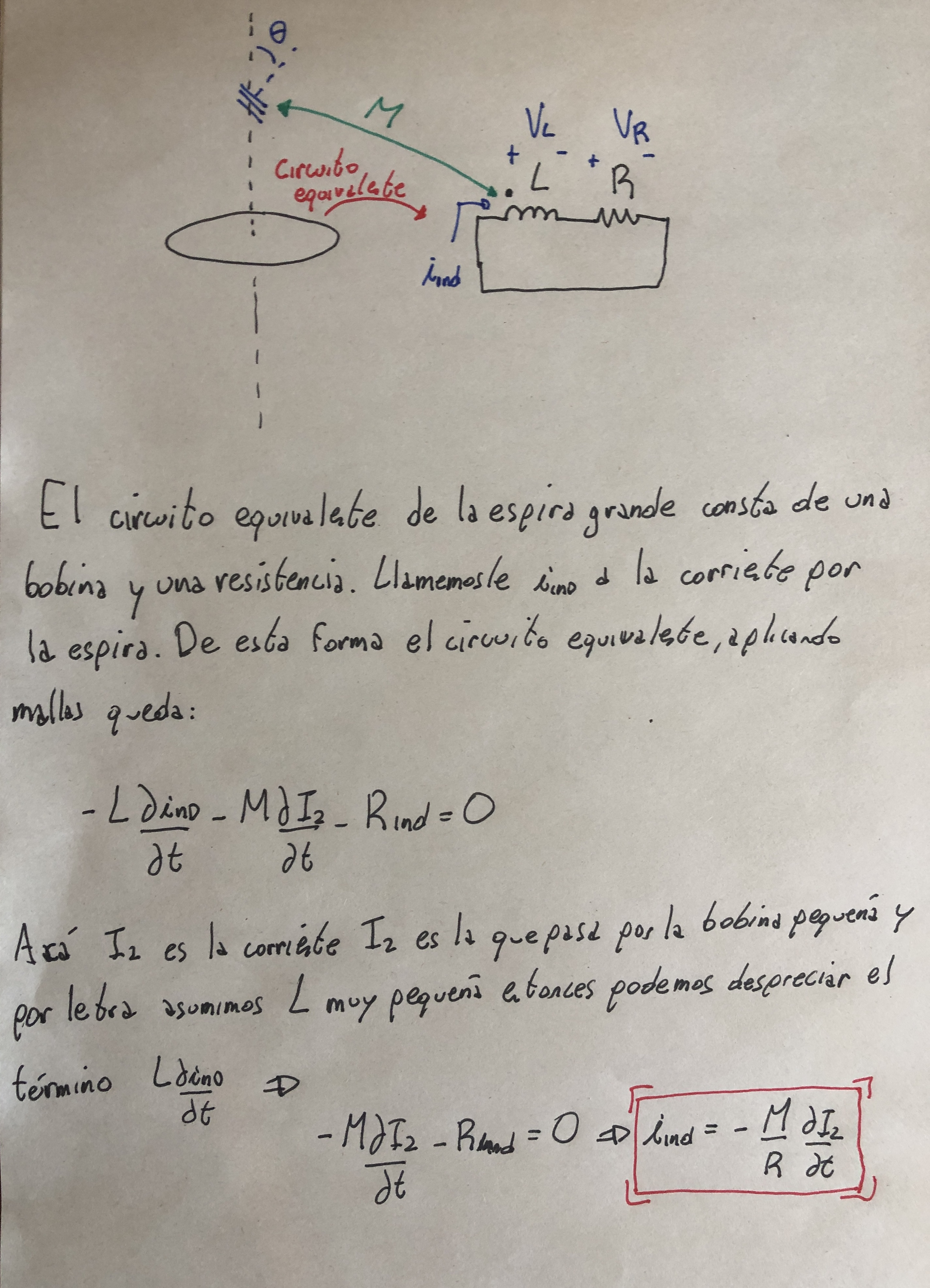
Te adjunto como quedaría el circuito equivalente de la espira grande, porque la relación que preguntas sale de aplicar la ley de mallas a ese circuito. Creo que la redacción del segundo párrafo me quedo más o menos, pero se entiende igual.
Espero que esto te aclare la duda, pero sino volvé a consultar sin problema.
Saludos,
Juan