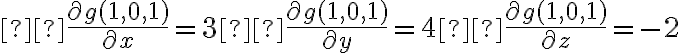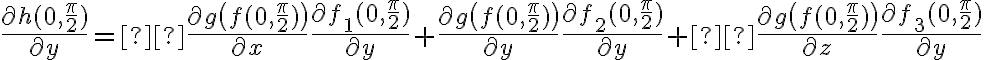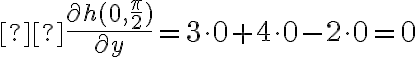Foro de Ejercicios fuera de los Prácticos

Buenas!

En este caso el gradiente nos da la información de las derivadas parciales de g en el punto 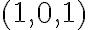$(1,0,1)$, es decir, sabemos:

$\frac{\partial g(1,0,1)}{\partial x} = 3 \phantom{aa} \frac{\partial g(1,0,1)}{\partial y} = 4  \phantom{aa} \frac{\partial g(1,0,1)}{\partial z} = -2$

Luego vemos que 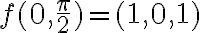$f(0,\frac{\pi}{2})=(1,0,1)$ entonces al darnos el gradiente nos dan la información de las derivadas parciales de $g$ evaluadas en $f(0,\frac{\pi}{2})$:

$\frac{\partial g\bigl(f(0,\frac{\pi}{2})\bigr)}{\partial x} = 3 \phantom{aa} \frac{\partial g\bigl(f(0,\frac{\pi}{2})\bigr)}{\partial y} = 4  \phantom{aa} \frac{\partial g\bigl(f(0,\frac{\pi}{2})\bigr)}{\partial z} = -2$

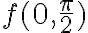Por la regla de la cadena teníamos que:

$\frac{\partial h(0,\frac{\pi}{2})}{\partial y} = \frac{\partial g\bigl(f(0,\frac{\pi}{2})\bigr)}{\partial x} \frac{\partial f_1(0,\frac{\pi}{2})}{\partial y} +\frac{\partial g\bigl(f(0,\frac{\pi}{2})\bigr)}{\partial y} \frac{\partial f_2(0,\frac{\pi}{2})}{\partial y} + \frac{\partial g\bigl(f(0,\frac{\pi}{2})\bigr)}{\partial z} \frac{\partial f_3(0,\frac{\pi}{2})}{\partial y}$

Por lo tanto evaluando en lo que vale cada derivada se obtiene:

$\frac{\partial h(0,\frac{\pi}{2})}{\partial y} = 3 \cdot 0 + 4 \cdot 0 - 2 \cdot 0 = 0$

Se podía ver que era cero de forma más fácil porque las derivadas de 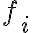$f_i$ según $y$ en el punto eran todas nulas.

Saludos!

Florencia