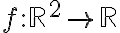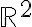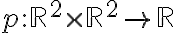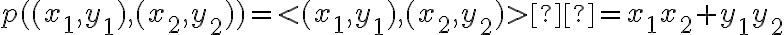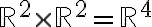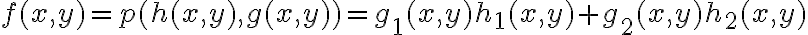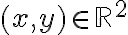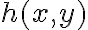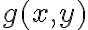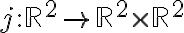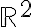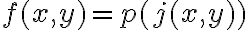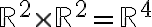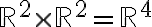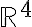15.e

15.e

de Agustín Arístides Almeida Ahlers -
Número de respuestas: 3

Buenas noches,

No comprendo de dónde sale la expresión de la matriz Jacobiana.

Entiendo que f(x,y) = g1(x,y) . h1(x,y) + g2(x,y) . h2(x,y) ¿pero cómo se interpreta esa expresión en términos del espacio de llegada y las derivadas parciales?

Desde ya gracias.

En respuesta a Agustín Arístides Almeida Ahlers

Re: 15.e

de Bernardo Marenco -
Hola. f es el producto interno entre g y h. Por lo tanto, f:\mathbb{R}^2 \to \mathbb{R}. Una forma de verlo es llamarle p a la función producto interno entre vectores de \mathbb{R}^2, es decir, p:\mathbb{R}^2 \times \mathbb{R}^2 \to \mathbb{R} está definida como p((x_1,y_1),(x_2,y_2)) = < (x_1,y_1),(x_2,y_2) >  = x_1x_2 + y_1y_2. Entonces, podés pensar que p va de \mathbb{R}^2 \times\mathbb{R}^2 = \mathbb{R}^4 a \mathbb{R}. Con esa notación, f(x,y) = p(h(x,y),g(x,y)) =g_1(x,y) h_1(x,y) + g_2(x,y) h_2(x,y).

Es decir, f es el resultado de, dado un (x,y)\in \mathbb{R}^2, encontrar los dos puntos de \mathbb{R}^2 dados por h(x,y) y g(x,y) y a esos puntos calcularle el producto interno. Entonces, si llamamos j:\mathbb{R}^2 \to \mathbb{R}^2 \times \mathbb{R}^2 a la función que, dado un (x,y)\in \mathbb{R}^2 me da dos puntos en \mathbb{R}^2 que son h(x,y) y g(x,y), tenemos que f(x,y)=p(j(x,y)), y por lo tanto podés pensar a f como la composición de una función de \mathbb{R}^2 a \mathbb{R}^2 \times \mathbb{R}^2 = \mathbb{R}^4 con otra de \mathbb{R}^2 \times \mathbb{R}^2= \mathbb{R}^4 a \mathbb{R}

Saludos
En respuesta a Bernardo Marenco

Re: 15.e

de Agustín Arístides Almeida Ahlers -
Buenas, comprendo la composición de funciones ahí, pero en la respuesta da a entender que va de R*2 a R*4, porque calcula las derivadas respecto a "x" e "y" de cada función y eso es lo que no comprendo ¿No debería quedar una matriz de una sola fila?
Saludos
En respuesta a Agustín Arístides Almeida Ahlers

Re: 15.e

de Bernardo Marenco -
Hola. La soluciónn da el resultado como el producto entre un vector de \mathbb{R}^4 y una matriz 4 \times 2. El resultado de ese producto es un vector de \mathbb{R}^2, que es coherente con que f vaya de \mathbb{R}^2 a \mathbb{R}.

Saludos