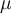Buenas, me queda una duda teórica. En la mayoría de los casos (incluido las clases grabadas) el problema dual se define como  / Sin embargo en las notas está planteado el caso general
/ Sin embargo en las notas está planteado el caso general  .
.
Para los casos en los que la función dual no tiene máximo, pero sí supremo, podemos obtener una solución del dual  , pero ese valor no se obtiene en la función dual, por lo que no existiría el multiplicador óptimo
, pero ese valor no se obtiene en la función dual, por lo que no existiría el multiplicador óptimo  ¿es correcto? Suponiendo que tenemos dualidad fuerte, podríamos obtener la solución del problema primal
¿es correcto? Suponiendo que tenemos dualidad fuerte, podríamos obtener la solución del problema primal 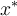 como el valor que minimiza el Lagrangiano para
como el valor que minimiza el Lagrangiano para  ¿cómo lo hacemos en este caso? ¿Tiene sentido estudiar el límite? ¿o no podemos obtenerlo? Gracias.
¿cómo lo hacemos en este caso? ¿Tiene sentido estudiar el límite? ¿o no podemos obtenerlo? Gracias.