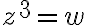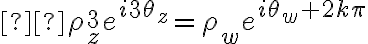Buenas!
Lo que estamos buscando es un número  tal que
tal que ![\sqrt[3]{w}=z \sqrt[3]{w}=z](https://eva.fing.edu.uy/filter/tex/pix.php/b089b82994a676960f4cd2eab8106e7b.gif) , es decir queremos hallar el número que multiplicado 3 veces por sí mismo nos dé como resultado
, es decir queremos hallar el número que multiplicado 3 veces por sí mismo nos dé como resultado 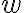 :
:
 tal que
tal que ![\sqrt[3]{w}=z \sqrt[3]{w}=z](https://eva.fing.edu.uy/filter/tex/pix.php/b089b82994a676960f4cd2eab8106e7b.gif) , es decir queremos hallar el número que multiplicado 3 veces por sí mismo nos dé como resultado
, es decir queremos hallar el número que multiplicado 3 veces por sí mismo nos dé como resultado 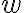 :
:Como estamos hablando de productos la notación que facilita estos cálculos es la polar, entonces planteamos 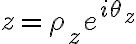 y
y 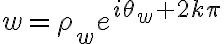 donde
donde  es un entero. Por lo que la ecuación anterior nos queda:
es un entero. Por lo que la ecuación anterior nos queda:
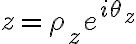 y
y 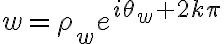 donde
donde  es un entero. Por lo que la ecuación anterior nos queda:
es un entero. Por lo que la ecuación anterior nos queda:Entonces por un lado obtenemos una ecuación para el módulo que nos da un único valor y por otro tenemos que igualar los exponentes de las exponenciales complejas que nos van a dar 3 posibles resultados, estas fases son las que nos dan las 3 distintas soluciones de la raíz cúbica compleja.
Saludos!
Florencia