Hola Juan,
Los vectores de norma 1, son vectores que al calcular su norma te da 1.
Además, de los dos que mencionas, podemos agregar: 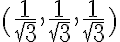
Se puede obtener un vector de norma 1, tomando el vector y dividiéndolo entre su norma.
Por ejemplo, tomamos el vector 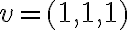 , calculamos la norma
, calculamos la norma 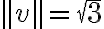 para conseguir un vector con la misma dirección, pero norma 1, hacemos lo siguiente:
para conseguir un vector con la misma dirección, pero norma 1, hacemos lo siguiente: 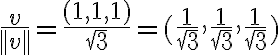
En el ejercicio lo que pide, primero, que encuentres el vector, perpendicular a u y v.
Una vez que se tiene el vector, conseguir uno, con igual dirección, pero de norma 1. Eso se logra, dividiendo el vector entre su norma.
Saludos,
Bettina.