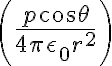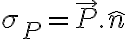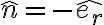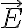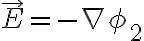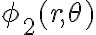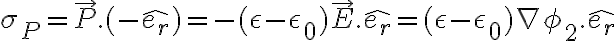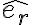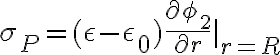Buenas, tengo varias dudas de este ejercicio.
1) En una respuesta anterior se dijo que el potencial debe ir a 0 en el infinito, a que se debe eso?
2) Al utilizar la condición del Dn utilicé que la carga libre sobre la superficie interfacial es 0 aunque no me quedó claro cuándo se cumple esa condición. En un ejercicio propuesto en clase la letra decía que había una esfera de un dieléctrico en el vacío y que la carga externa es 0 aunque entonces ahí la tomamos cero, pero acá la letra no dice nada.
3) Que seria carga inducida? La de polarización? En ese caso tendria que hacer n.P donde n = -er con er saliente y luego D = Ɛ0E + P y acá me confundo pila con las direcciones, el E me queda E= (6Pcosθ)/(4π(2Ɛ+Ɛ0)r3) y la direccion no se bien cual es aunque se me ocurrió poner Pcosθ= Per pero no se.
Gracias!!