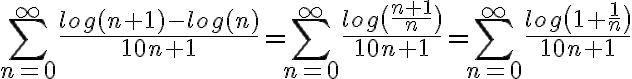Buenas!
En este caso tenemos la serie:
Utilizando propiedades de los logaritmos podemos reescribir esta expresión de una forma que nos sea más cómoda:
Ahora podemos ver el límite cuando 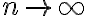 de la sucesión, el término
de la sucesión, el término 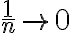 dentro del logaritmo, por lo que se puede aplicar el criterio de equivalentes (cuando
dentro del logaritmo, por lo que se puede aplicar el criterio de equivalentes (cuando 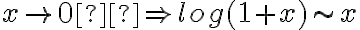 ) por lo que
) por lo que  , en ese caso tendríamos que
, en ese caso tendríamos que 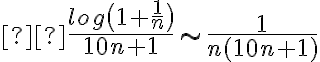 y así es más fácil ver que este límite es equivalente a
y así es más fácil ver que este límite es equivalente a 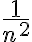
Si así sigue sin parecer claro lo vemos de otra forma :)
Saludos!
Florencia