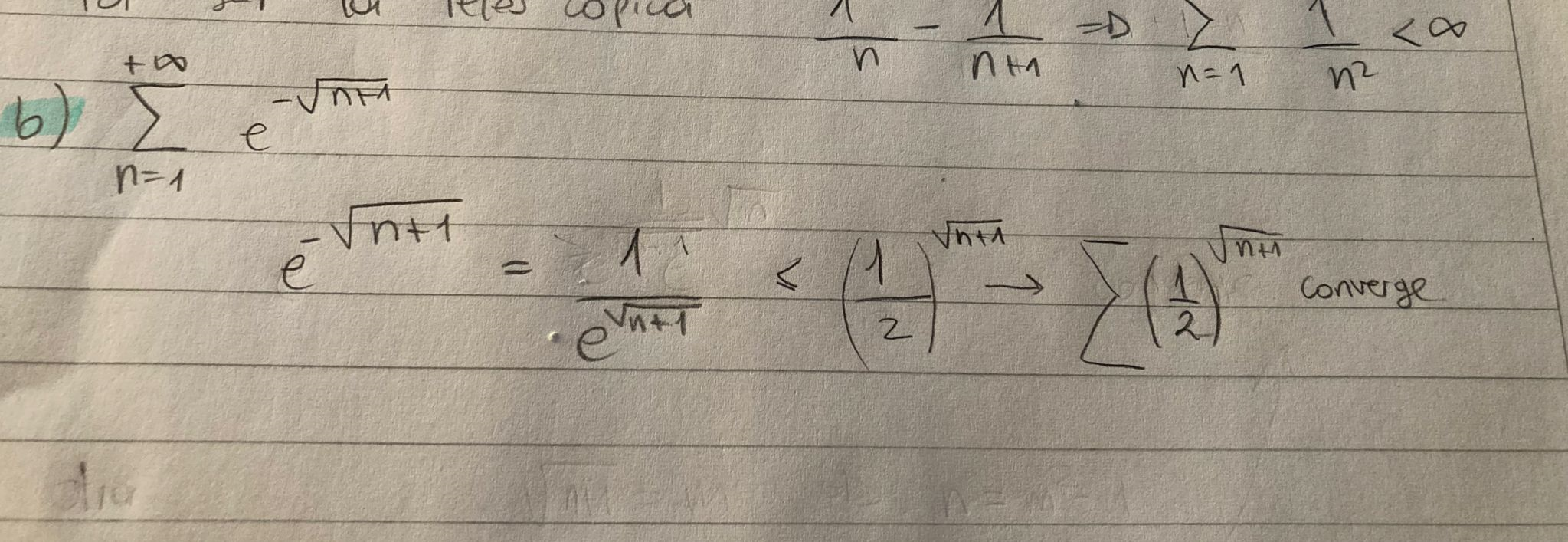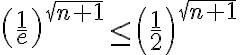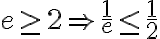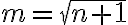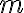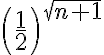Buenas tardes, quisiera sanber si esta bien realizar esta comparación, pensando serie mayor como una geométrica, porque si aplicara un cambio de variable podria pasar la raiz a una m simple, y que la serie continúe iniciando en un natural, que sería en este caso cero.
Hola. La desigualdad 
es cierta, porque 
. Igual, ojo con el cambio de variable que decís, porque si llamás 
entonces 
no necesariamente es natural, y no tenemos herramientas para clasificar sumas de cosas cuya variable no es natural. Tendrías que buscar otro argumento para probar que la serie de 
converge.
Saludos