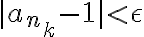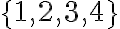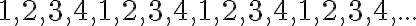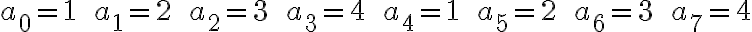Buenas!
En ese caso queremos una sucesión que contenga subsucesiones convergentes a
que contenga subsucesiones convergentes a 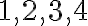 , que es lo mismo que pedir que estos valores sean puntos de acumulación.
, que es lo mismo que pedir que estos valores sean puntos de acumulación.
En ese caso queremos una sucesión
 que contenga subsucesiones convergentes a
que contenga subsucesiones convergentes a 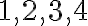 , que es lo mismo que pedir que estos valores sean puntos de acumulación.
, que es lo mismo que pedir que estos valores sean puntos de acumulación.De esta forma los
 con
con  valen siempre 1 y por lo tanto convergen a 1 (por ser constante), los
valen siempre 1 y por lo tanto convergen a 1 (por ser constante), los  con
con 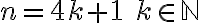 valen
valen 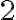 y por tanto convergen a
y por tanto convergen a 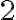 y así sucesivamente. Aparecen en este caso los múltiplos de 4 por tratarse de 4 puntos de acumulación.
y así sucesivamente. Aparecen en este caso los múltiplos de 4 por tratarse de 4 puntos de acumulación.Saludos!!
Florencia