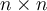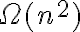En el practico 2 nos piden analizar la solución al algoritmo de Gale-Shapley indicada en el libro.
El libro separa el algoritmo en 4 partes y para solucionar la 4ta parte (que referencia a como comparar en tiempo O(1) la preferencia de una mujer frente a dos hombres m y m') nos plantea crear una matriz n x n donde se guardan las preferencias de las mujeres, permitiendo cumplir con la condición solicitada.
Pero esta solución me platea la siguiente duda: si bien es claro que se cumple la condición de comparar la preferencia de 1 mujer frente a 2 hombres en tiempo O(1), nos genera una demora (por fuera del algoritmo en si) que es cargar todos los datos en la matriz n x n, que según entiendo sería en tiempo n^2
No debemos considerar estos tiempos a la hora de analizar un algoritmo?
O, dicho de otra manera, podemos plantear que un problema se soluciona utilizando una estructura dada sin preocuparnos mucho por la demora de dicha estructura? O como deberíamos manejar esto?
Gracias.