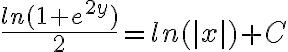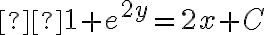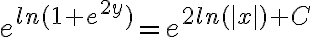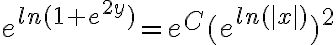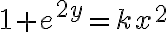Foro Práctico 2

Buenas!

Lo que hiciste está muy bien, el único problema está en el pasaje: 

$\frac{ln(1+e^{2y})}{2} = ln(|x|) + C$

$1+e^{2y} = 2x + C$

El problema está en el 2x, ya que el dos debería ser el exponente de una e también, es decir, el procedimiento sería:

$\frac{ln(1+e^{2y})}{2} = ln(|x|) + C$

$ln(1+e^{2y}) = 2ln(|x|) + C$

$e^{ln(1+e^{2y})} = e^{2ln(|x|) + C}$

$e^{ln(1+e^{2y})} = e^C (e^{ln(|x|)})^2$

$1+e^{2y} = k x^2$

Y siguiendo los mismos pasos desde ahí llegan a la solución. También se podían aplicar las propiedades de logartimo y utilizar que 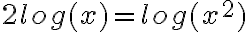$2log(x)=log(x^2)$

Saludos!!

Florencia :)