Buenas!
Queremos resolver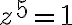 entonces tenemos que escribir ambos lados de la igualdad en notación polar.
entonces tenemos que escribir ambos lados de la igualdad en notación polar.
Queremos resolver
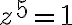 entonces tenemos que escribir ambos lados de la igualdad en notación polar.
entonces tenemos que escribir ambos lados de la igualdad en notación polar.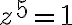 entonces tenemos que escribir ambos lados de la igualdad en notación polar.
entonces tenemos que escribir ambos lados de la igualdad en notación polar.