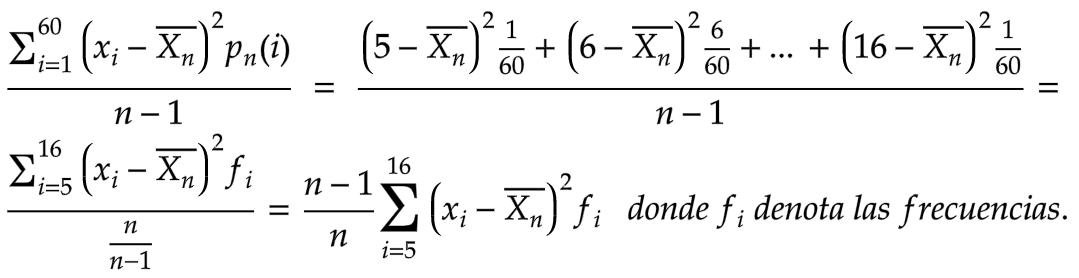EJ 3.1 - Examen Julio 2016.

EJ 3.1 - Examen Julio 2016.

de Marco Liguori Hernandez -
Número de respuestas: 7

Buenas,

No estoy entendiendo como calcular la varianza muestral en el caso como el del ejercicio.


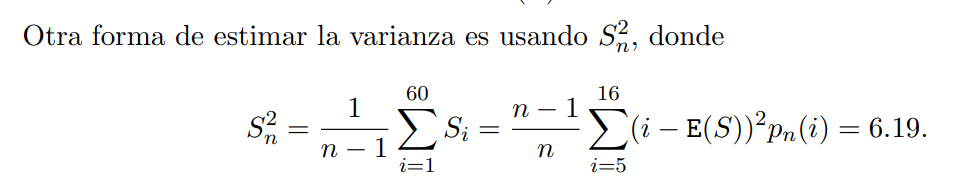
No entiendo esta solución pero además tampoco entiendo como se ejecutaría el cálculo en los casos que nos dan una muestra con frencuencias como es en este caso. En la solución también plantea que la varianza es igual a la esperanza porque es una Poisson, pero quisiera saber como calcular Sn^2. Supuse que era, por cada i, restar la (frencuencia x nro incrementos en el mes - el promedio muestral) ^ 2 y luego divido entre N-1, pero de esa forma no llego al resultado y me da uno mucho mayor al real.

Desde ya muchas gracias,

Marco.

En respuesta a Marco Liguori Hernandez

Re: EJ 3.1 - Examen Julio 2016.

de Eduardo Canale -
Lo que hace allí es aplicar la definición de la varianza \(\mathbb{V}(X) = \mathbb{E}(X-\mathbb{E}X)^2\) y usar la fórmula de la esperanza de \( f(X) \) siendo \( X \) discreta, con \( f(x) = (x - \mu^2)\) siendo \(\mu = \mathbb{E}X\).
Como sabes, la fórmula para espera de \( f(X) \) siendo \( X \) discreta, es
\( \sum_{x \in Rec(X)} (x-\mu^2)^2 p_X(x) \).
De todas formas la fórmula debería multiplicar por \(\frac{n}{n-1}\) y no por \(\frac{n-1}{n}\), además esa sumatoria de \(S_i \) es muy confusa, porque se confunde con la desviación empírica. En fin, la cuenta debería ser:
\(S_n^2 = \frac{n}{n-1} \sum_{i =1}^{\infty} (i- \mathbb{E}(S))^2 p_n(i)\).

Saludos
En respuesta a Eduardo Canale

Re: EJ 3.1 - Examen Julio 2016.

de Marco Liguori Hernandez -
Buenas Eduardo,

Haciendo las cuentas y siguiendo lo que me comentas, me estaba costando entender de dónde salía el n que multiplicaba toda la sumatoria (y que es dividido por n-1 que corresponde a la definición de varianza muestral ajustada). Me doy cuenta que en realidad esa sumatoria está encerrada por otra que va desde j = 1 hasta j = 60 ¿verdad?. En ese caso no me doy cuenta porqué se suma 60 veces la sumatoria que iría desde i = 5 hasta i = 16 (ya que el recorrido de la muestra es {5,6,...,16}).

Si me orientas con eso te agradezco.

Saludos, Marco.
En respuesta a Marco Liguori Hernandez

Re: EJ 3.1 - Examen Julio 2016.

de Eduardo Canale -
Hola Marco, ojo que la sumatoria que va hasta 60 no encierra a la otra.
La de 60 es un promedio (aunque dividido por 59, la otra es otra cosa.
Digamos que en la que suma hasta 16 (que en realidad va hasta infinito, pero hay términos que no aparecen porque hay p_i =0), el promedio está en las probabilidades.
En respuesta a Eduardo Canale

Re: EJ 3.1 - Examen Julio 2016.

de Marco Liguori Hernandez -
Buenas Eduardo,

Revisando lo que me comentas, creo entender de dónde sale el 'n' pero me estaría quedando igual a la solución.


¿Dónde está el error aquí?.

Muchas gracias, 
Marco.
En respuesta a Marco Liguori Hernandez

Re: EJ 3.1 - Examen Julio 2016.

de Eduardo Canale -
Hola Marco, en tu razonamiento hay tres puntos que no entiendo:
1) primero la fórmula inicial, porque dividís entre (n-1) pero adentro de la fórmula aparecen probabilidades. En realidad cuando calculás la esperanza de algo, por ejemplo de \((X-\mathbb{E}(X))^2\) que sería la varianza, deberías hace un primedio de las \((X_i-\mathbb{E}(X))^2\), pero en ese caso, sumarías hasta 60 (pues n = 60) y dividirías entre n = 60.
2) En la primer igualdad, no sé como justificas ese pasaje. Porque pasas de sumar 60 valores a sumar 16 ¿no?
3) En el pasaje de la segunda fórmula. la tercera, o sea, la segunda igualdad, aparece un "n", y el "n-1" lo pasaste a dividir en el denominador.
Bueno, es lo que veo a simple vista.
Saludos
En respuesta a Eduardo Canale

Re: EJ 3.1 - Examen Julio 2016.

de Eduardo Canale -
Hay otra forma de ver como se pasa de la suma hasta \(n\) y las frecuencias que es así: si
\(\{x_1,\ldots, x_n \} = \{a_1,\ldots, a_r\}\) con \(a_1 < a_2 < \cdots < a_r\), o sea que los \( a_i \) son los valores qeu toman las \( x_i\) sin repetir, entonces
\(\frac{1}n \sum_{i=1}^n x_i = \frac{1}n \sum_{j=1}^r a_j |\{i: x_i = a_j\}|
= \sum_{j=1}^r a_j \frac{|\{i: x_i = a_j\}|}n
= \sum_{j=1}^r a_j f_j
\) siendo \( f_j = \frac{|\{i: x_i = a_j\}|}n \) la frecuencia con que se toma el valor \( a_j \).