Hola,
Efectivamente, como menciona el compañero, hay que tener cuidado que el punto A está acelerado porque la placa se mueve horizontalmente. La fórmula completa de la segunda cardinal es
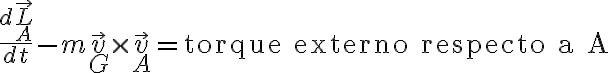
siendo
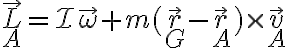
Para el rígido en traslación pura se tiene que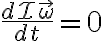 y entonces tenemos
y entonces tenemos
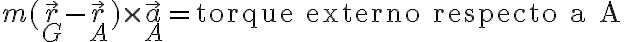
Usando que en este ejercicio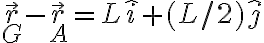 y
y 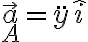 entonces se llega a la fórmula que aparece en la solución:
entonces se llega a la fórmula que aparece en la solución:

Espero que esto aclare las cosas. De lo contrario no duden en volver a preguntar.
Saludos
Guzmán
Efectivamente, como menciona el compañero, hay que tener cuidado que el punto A está acelerado porque la placa se mueve horizontalmente. La fórmula completa de la segunda cardinal es
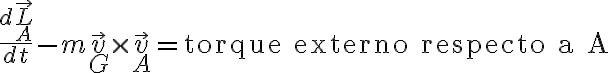
siendo
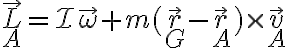
Para el rígido en traslación pura se tiene que
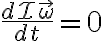 y entonces tenemos
y entonces tenemos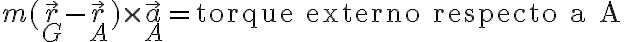
Usando que en este ejercicio
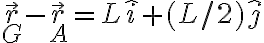 y
y 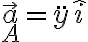 entonces se llega a la fórmula que aparece en la solución:
entonces se llega a la fórmula que aparece en la solución:
Espero que esto aclare las cosas. De lo contrario no duden en volver a preguntar.
Saludos
Guzmán
