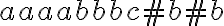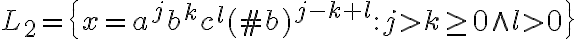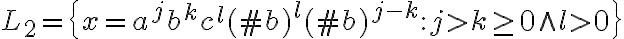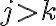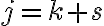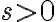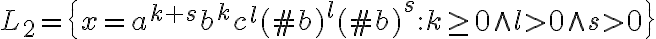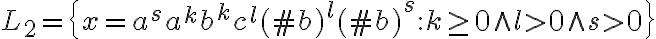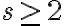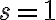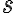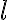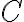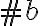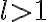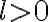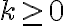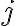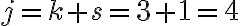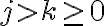En la solución de la parte b las reglas de derivación son:
S -> aS#b | XC#b
X -> aXb | a
C -> cC#b | c#b
La duda es como controla que por cada par de ab que tengo en X tenga dos #b porque según el lenguaje por cada a o b tiene que haber un #b
Por ejemplo con estas regla de derivación se derivar la tira aaaabbbc#b#b