Hola que tal? No entiendo como se llega a la solución de este ejercicio. Agradezco me puedan esclarecer la duda.

Hola que tal? No entiendo como se llega a la solución de este ejercicio. Agradezco me puedan esclarecer la duda.

Buenas
Podemos ir viendo esto en cada condicion. Esto se puede hacer pues el conjunto  es relativamente chico.
es relativamente chico.
Condición 0) Primero el diagrama de Hasse sean 4 cadenas disjuntas de tamaño 3 representa que hay 4 subconjuntos de A totalmente ordenados
Si esta fuera la única restricción la cantidad de relaciones seria: elegir los subconjuntos por cantidad de relaciones de orden total en cada uno. Es decir
Donde los numeros corresponden a las siguientes elecciones
 corresponde a la elección de los elementos en la cadena
corresponde a la elección de los elementos en la cadena 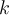
Cada  corresponde a ordenar cada cadena
corresponde a ordenar cada cadena
y la división  corresponde a que en realidad el orden de las cadenas no importa.
corresponde a que en realidad el orden de las cadenas no importa.
Condición 1) Al agregar la condicion de minimalidad tenemos que la forma de elegir los subconjuntos ya marca que siertos numeros no pueden estar juntos (1 y 3 por ejemplo). Al tener todos los minimales podemos elegir cuales son otros que estan en cada subconjunto (cuales son mayores al 1 por ejemplo) y ordenar estos (pues los primeros ya estan definidos). Esto da:
Cada  corresponde a elegir los elemntos de la cadena que tiene a
corresponde a elegir los elemntos de la cadena que tiene a  , con los anteriores ya elegidos
, con los anteriores ya elegidos
Esta vez no aparece el 4! dividiendo pues las cadenas ya no son inindistinguibles (pues el minimal de cada cadena esta fijo)
Condicion 2) Al marcar los elementos maximales tenemos una descripción completa de cuales son las posbilidades es decir cada cadena debe tener exactamente un elemento de cada un de los siguientes conjuntos  .
.
Por lo que para contar podemos hacer loi siguiente, primero decidir cual de los elementos de 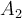 y
y  van a ser mayores que el 1 y como los de A_{3} son los maximales no hay eleccion posible para el orden. Si por ejemplo elegimos el 6 y el 10 esa cadena debe ser
van a ser mayores que el 1 y como los de A_{3} son los maximales no hay eleccion posible para el orden. Si por ejemplo elegimos el 6 y el 10 esa cadena debe ser  . Repitiendo los argumentos de los casos anteriores tenemos que la cantidad de opciones es
. Repitiendo los argumentos de los casos anteriores tenemos que la cantidad de opciones es
Condición 3) Esta condicion solo quita una opcion posible para la eleccion de la cadena del 1, es decir la formula es
Cualquier cosa vuelve a escribir
Saludos