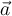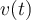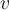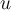F1 - 1S: Teorema Trabajo/Energía - Demostración

Hola, quería consultar unas dudas que me vinieron releyendo algunas cosas en Resnick.

En el capítulo que habla sobre el teorema de la Energía y el Trabajo, hace una demostración general del teorema y se ven una serie de detalles que no entiendo bien.

Duda 1) En la demostración se utiliza la 2da Ley de Newton, por lo que que como Fneta=m.a, entonces F=m(dv/dt), luego se hace algo que no comprendo, es como si multiplicara y dividiera por dx, de forma que F=m(dv.dx/dx.dt), logrando así obtener la velocidad y por otro lado la expresión dv/dx.
¿Este procedimiento de hacer aparecer el dx como un número es puramente algebraico o tiene alguna justificación desde la física?
Además, tampoco entiendo cómo se multiplica y divide por algo que no es "nada", es decir, el dv o el dx es notación para indicar la derivada, no sabía que fuera un elemento algebraico.
En cualquier caso, ¿Qué significa dv/dx? ¿Qué significado físico tiene?

Duda 2) En el libro se hace una prueba general del teorema y explicita concretamente que este teorema funciona incluso para fuerzas no constantes. No entiendo cómo esto es posible, debido a que estamos utilizando la 2da ley de Newton, que por lo que entiendo (capaz entendí mal) es verdadera solamente para fuerzas constantes, ya que vincula una aceleración única asociada a esa fuerza neta durante un cierto tiempo que dura un cierto evento. ¿Es así?

Saludos y gracias como siempre. Sí, soy el de las preguntas teóricas largas :(

Re: Teorema Trabajo/Energía - Demostración

de Carla Yelpo - martes, 21 de junio de 2022, 14:53

Hola, Diego

Voy a responder empezando por el final.

Sobre la duda 2:

La segunda ley de Newton vale también cuando las fuerzas son variables en el tiempo. Si tenemos un cuerpo sobre el cual se aplica una fuerza neta variable, al aplicar la segunda ley de Newton simplemente obtendremos que la aceleración también es variable. Es decir, nos quedaría:

$\vec{F}_{neta}(t) = m \vec{a}(t) \Rightarrow \vec{a}(t) = \frac{\vec{F}_{neta}(t)}{m}$

Donde tanto $\vec{F}_{neta}$ como $\vec{a}$ dependen del tiempo.

Sobre la duda 1:

La demostración que se hace en el Resnick, comienza haciendo la siguiente consideración. En vez de escribir a la velocidad como una función del tiempo $v(t)$ , se considera a la velocidad como una función de la posición, que a su vez es una función del tiempo: $v(x(t))$ .

[Esto lo podemos hacer sin inconveniente. Fijate, por ejemplo, la ecuación 20 del capítulo 2 del Resnick, donde se escribe la velocidad como función de la posición para el caso de un movimiento rectilíneo uniformemente acelerado.]

Entonces, cuando hacemos la derivada de esta función compuesta respecto al tiempo, debemos aplicar la regla de la cadena: $(v \circ x) ' = v'(x(t))x'(t)$

Eso es lo que está haciendo en la primer línea, cuando reescribe la fuerza neta.

Luego, cuando escribe el trabajo neto, lo que hace es aplicar el método de integración por cambio de variable. Consideremos una función de la velocidad $f(v) = mv$ , siendo $v$ una función de la posición $v(x)$ . Entonces, podemos escribir el trabajo como:

$W_{neto} = \int f(v)v'(x)dx$

Y definiendo el cambio de variable $u = v(x)$ , podemos re-escribirlo como:

$W_{neto} = \int f(u)du$

En el libro se hace un ligero abuso de notación, y a la "nueva variable" $u$ le da el mismo nombre $v$ que teníamos antes. Pero la justificación detrás es aplicar este método.

Te dejo acá un enlace a la demostración del método de integración por cambio de variable. En definitiva, lo que estamos haciendo con esto es mostrar que es posible manipular los diferenciales de manera algebraica cuando hacemos estos cambios de variable. Pero no porque se traten de un número, sino que, como verás en la demostración, es el resultado de aplicar la regla de la cadena y el teorema fundamental del cálculo.

Espero que esto ayude. Cualquier cosa volvé a preguntar.

¡Saludos!

Re: Teorema Trabajo/Energía - Demostración

de Diego Subeldia Loureiro - miércoles, 22 de junio de 2022, 07:49

Qué maravilla Carla! Quedó clarísimo
Menudo detalle el de F(t)=ma(t), no me lo sabía, quiero decir, nunca había visto una formulación así en función del tiempo ni sospechaba que eso fuese válido.
Y no me daba cuenta que había aplicado regla de cadena para derivar y cambio de variable para integrar. Ambas herramientas ya las vimos en Cálculo, pero no sé, no até cabos.
Muchas gracias!!