Hola estoy intentando resolver este ejercicio usando las cardinales pero al momento de utilizar la segunda cardinal no estoy seguro de como escribir el momento que realiza la normal en la cara AB de la placa triangular. Si me pueden dar una mano les agradezco. Saludos!
Hola, primero que nada tenes que ver que como tenes dos superficies de contacto, las fuerzas de acción-reacción (que serian las normales) son un conjunto infinito de normales. Para simplificar el problema, lo que se hace es sumar todas esas normales y transformarlas en una sola. Si te preguntas a que distancia se encuentra esa normal, la respuesta es a una distancia arbitraria de A o de B, por ejemplo: si haces segunda cardinal desde B te recomiendo que coloques a esa normal a una distancia x de B.
Espero haber aclarado y no oscurecido
Espero haber aclarado y no oscurecido
Hola,
La aclaración es correcta. En principio uno tendría "infinitas normales" en ese contacto, que las condensa en una única normal en un pto de aplicación desconocido, por ejemplo a una distancia "x" del pto B. Esta x es una de las incógnitas que vamos a tener que hallar resolviendo las condiciones de estática (sumatoria de fuerzas igual a cero y sumatoria de momentos igual a cero).
Una vez a hallada la x y las demás reacciones tenemos que imponer sobre estas las condiciones de que la estática efectivamente sea posible, es decir las condiciones de no desprendimiento, no deslizamiento y no vuelco. Por ejemplo, la condición de no vuelco sobre la x es que x este entre 0 y L, o equivalmentemente, que el pto de aplicación de la normal sea dentro de la cara AB.
Espero que esto aclare las cosas. De lo contrario no duden en volver a preguntar.
Saludos
Guzmán
La aclaración es correcta. En principio uno tendría "infinitas normales" en ese contacto, que las condensa en una única normal en un pto de aplicación desconocido, por ejemplo a una distancia "x" del pto B. Esta x es una de las incógnitas que vamos a tener que hallar resolviendo las condiciones de estática (sumatoria de fuerzas igual a cero y sumatoria de momentos igual a cero).
Una vez a hallada la x y las demás reacciones tenemos que imponer sobre estas las condiciones de que la estática efectivamente sea posible, es decir las condiciones de no desprendimiento, no deslizamiento y no vuelco. Por ejemplo, la condición de no vuelco sobre la x es que x este entre 0 y L, o equivalmentemente, que el pto de aplicación de la normal sea dentro de la cara AB.
Espero que esto aclare las cosas. De lo contrario no duden en volver a preguntar.
Saludos
Guzmán
Sobre el ejercicio, me surgió una pregunta y es mas orientada a un práctico anterior. Para hayar el centro de masa de la placa triangular use simetría pero luego cuando lllego a la parte de integrar tengo la duda de el diferencial de area(dA) en el caso del triángulo que sería. (dX.dY)/2? Y la densidad de area como la elimino?
Buenas tardes, Dan.
En coordenadas cartesianas, el diferencial de área es dxdy.
No entiendo bien a qué te referís con 'eliminar la densidad de área'. La densidad de masa se define como la masa total sobre el área total de la placa.
Saludos!
En coordenadas cartesianas, el diferencial de área es dxdy.
No entiendo bien a qué te referís con 'eliminar la densidad de área'. La densidad de masa se define como la masa total sobre el área total de la placa.
Saludos!
Hice el ejercicio pero no encuentro el error me falta un raíz de 2 en la solución para x. Espero se entienda gracias
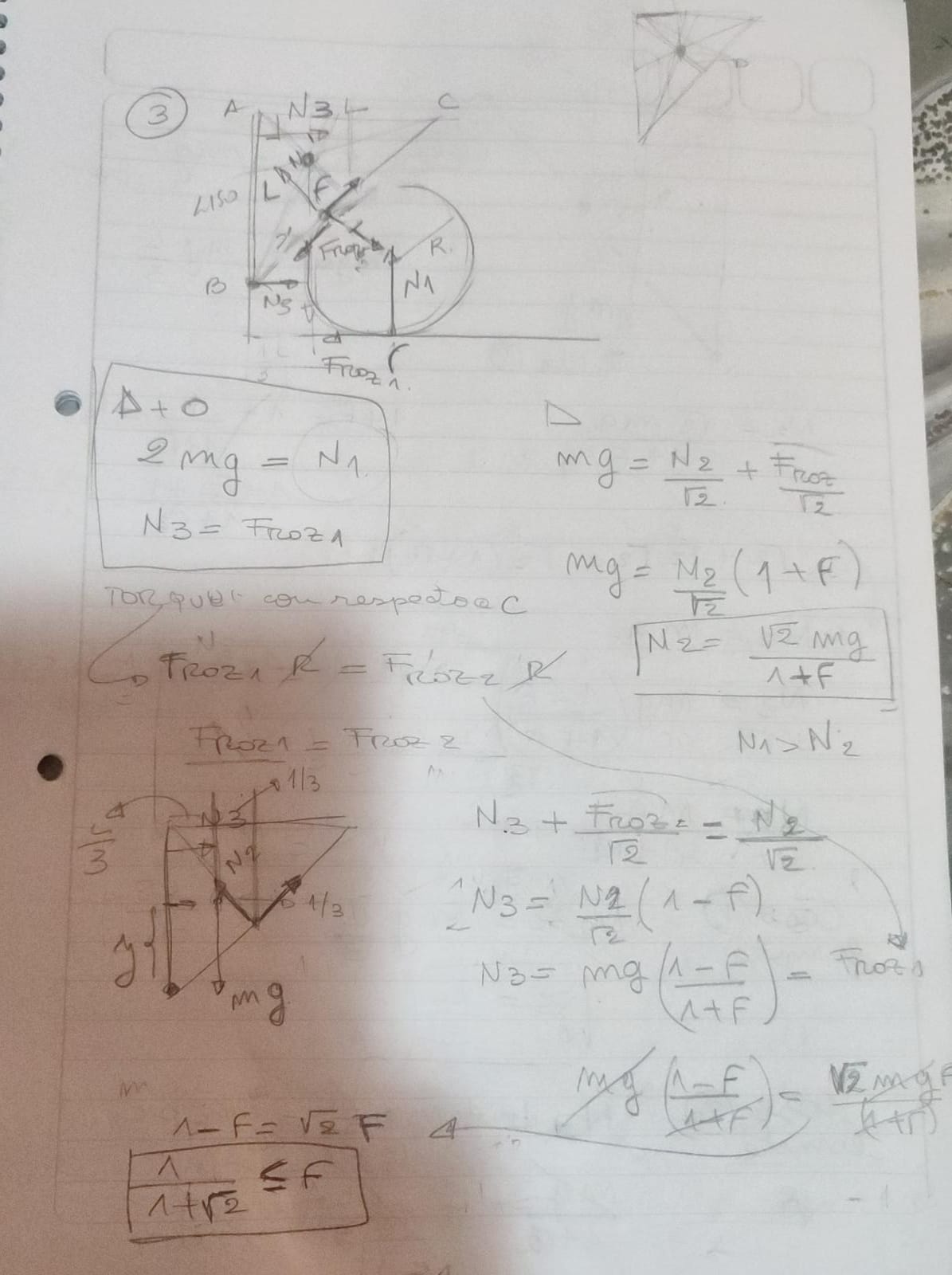

Buenas Elena.
La letra del ejercicio dice que la discusión debe darse en función de la distancia del punto D (punto de contacto entre la placa y el disco) a la pared. Si no interpreto mal, esa no es la distancia a la que estás llamando x, ¿verdad?
Saludos!
A claro!!! Que Pancha!! Siempre leyendo mal la letra gracias.
