Buenas, tengo unas dudas
con respecto al ejercicio 4, lo empecé planteando las cardinales y llegue a intervalos a los que podría corresponder alfa y beta pero no llegue explícitamente a lo que dice la solución, luego plantee energía porque leí en un foro que dieron esa sugerencia pero tampoco llegue porque yo lo plantee el centro de masa de la barra desde A.
Con respecto al ejercicio 5, lo hice por energía, (asumí que el centro de masa de las barras esta en el centro del "rombo" eso esta bien? )
Luego llegue a la ecuación que esta en la solución del practico con el alfa para despejar y pensé que ahí terminaba el ejercicio, pero aparece algo de que alfa tiene que ser el máximo entre ese alfa que habría que hallar y un termino de arcsen que no se de donde sale.
Hola, Valentina
no entiendo la duda del ejercicio 4. Dado que el sistema es conservativo buscar mínimos relativos de la energía potencial es una buena opción.
Con respecto al 5, el centro de masa efectivamente en el centro del rombo, lo podés demostrar fácilmente.
En la solución se estudia en adición el caso en que el rombo "aprieta" al disco de adentro. El alfa delrombo no puede achicarse más que eso (alfa_min), dado que el disco es rígido. De ahí sale la cota para alfa.
Saludos
no entiendo la duda del ejercicio 4. Dado que el sistema es conservativo buscar mínimos relativos de la energía potencial es una buena opción.
Con respecto al 5, el centro de masa efectivamente en el centro del rombo, lo podés demostrar fácilmente.
En la solución se estudia en adición el caso en que el rombo "aprieta" al disco de adentro. El alfa delrombo no puede achicarse más que eso (alfa_min), dado que el disco es rígido. De ahí sale la cota para alfa.
Saludos
Buenas, yo tengo unas dudas respecto al ejercicio 4.
Para decir que el sistema es conservativo, tengo que probar que las fuerzas derivan de un potencial, o bien son de potencia nula, no? No me doy cuenta si puedo decir que la normal y la tensión son de potencia nula porque no hay movimiento en el sistema, y con ello, los puntos donde están aplicadas las fuerzas tienen velocidad 0.
Mi otra duda es que cuando planteo con cardinales, llego a unos intervalos posibles para alpha y beta, pero no logro llegar a lo que dice la solución. Tuve un problema a la hora de plantear el momento, cuando lo planteo desde A, ese momento puedo imponer que me de 0, si en lugar de plantearlo desde A, lo planteo desde el CM o bien desde B, ese momento nunca es 0, esto por qué se da?
A las condiciones que llegué cuando plantee la 1ra cardinal fueron:
T=mg/(cos(alpha))
N=mgtan(alpha)
Mientras que de la segunda, obtuve:
2tan(alpha)=-tan(beta)
De la geometría del problema, use que:
2lsen(beta)=2asen(alpha)
Mis condiciones de equilibrio puse que eran N>=0, T>=0, hallando así un posible intervalo para alpha y uno posible para beta.
Creo que entiendo por que la solución solo admite los ángulos que admite, pero no me doy cuenta que relación tengo que plantear para obtener esos ángulos.
Gracias, saludos!
Para decir que el sistema es conservativo, tengo que probar que las fuerzas derivan de un potencial, o bien son de potencia nula, no? No me doy cuenta si puedo decir que la normal y la tensión son de potencia nula porque no hay movimiento en el sistema, y con ello, los puntos donde están aplicadas las fuerzas tienen velocidad 0.
Mi otra duda es que cuando planteo con cardinales, llego a unos intervalos posibles para alpha y beta, pero no logro llegar a lo que dice la solución. Tuve un problema a la hora de plantear el momento, cuando lo planteo desde A, ese momento puedo imponer que me de 0, si en lugar de plantearlo desde A, lo planteo desde el CM o bien desde B, ese momento nunca es 0, esto por qué se da?
A las condiciones que llegué cuando plantee la 1ra cardinal fueron:
T=mg/(cos(alpha))
N=mgtan(alpha)
Mientras que de la segunda, obtuve:
2tan(alpha)=-tan(beta)
De la geometría del problema, use que:
2lsen(beta)=2asen(alpha)
Mis condiciones de equilibrio puse que eran N>=0, T>=0, hallando así un posible intervalo para alpha y uno posible para beta.
Creo que entiendo por que la solución solo admite los ángulos que admite, pero no me doy cuenta que relación tengo que plantear para obtener esos ángulos.
Gracias, saludos!
Estimado:
Exacto: para decir que el sistema es conservativo hay que probar que las fuerzas son conservativas o de potencia nula. No vale decir que las fuerzas son de potencia nula porque la velocidad es cero, porque hay que estudiar el sistema en movimiento. Si se considera como sistema la barra tenemos:
1) El peso es conservativo.
2) La normal en la pared es de potencia nula porque el extremo A de la barra (mientras permanezca apoyado) se mueve en la dirección vertical y la reacción es horizontal porque no hay rozamiento. Por lo tanto la velocidad y la fuerza son perpendiculares, su producto escalar es cero y es de potencia nula. Si hubiese rozamiento no sería el caso: la fuerza en A no es de potencia nula y el sistema no es conservativo.
3) La tensión en B también es de potencia nula, porque mientras el hilo esté estirado B recorre una circunferencia de radio 2a respecto al punto de unión del hilo con la pared. Y la tensión del hilo es según la normal a esta circunferencia. La velocidad como siempre será tangente. De nuevo el producto escalar es nulo.
4) Y después las otras fuerzas que hay que considerar son las fuerzas internas de la barra (que la mantienen unida). Pero en teórico se demostró que las fuerzas internas de un rígido son de potencia nula por el principio de acción y reacción fuerte.
Otro punto de vista sería considerar el sistema barra más hilo. Aquí el hilo se comporta como una barra rígida de masa nula, por lo que sus fuerzas internas también son de potencia nula. Pero además de las fuerzas anteriores hay que considerar la tensión del hilo en el punto de unión entre el hilo y la pared, y esta sí es de potencia nula porque este punto siempre está fijo. También aparece la reacción de la tensión en B actuando sobre el hilo, pero también es de potencia nula porque por acción y reacción es opuesta a la anterior y el punto B del hilo tiene la misma velocidad que el punto B de la barra.
En relación a tu método de aplicar cardinales creo que todas las ecuaciones que planteas son correctas. Pero la condición de equilibrio no sale de hacer T y N mayores o iguales que cero, ya que de tus ecuaciones se ve que ambas son postivas (o nulas), ya que alpha es mayor o igual que cero pero menor que π/2.
La condición de equilibrio sale de la relación 2tan(alpha)=-tan(beta). Hay que escribir estas tangentes en función de los senos de los ángulos, y luego sustituir sen(beta) de la relación 2lsen(beta)=2asen(alpha).
Saludos:
Ricardo.
Buenas, gracias por la respuesta, me quedó todo bastante claro, salvo la última parte, comprendo lo que planteas del ejercicio 5 del práctico 5, pero en este caso no me estaría quedando que se cumple eso, seguro le estoy errando en algo.
Cuando planteo desde el CM (a una distancia l de la recta AB), obtengo que el momento que aporta la normal es positivo (saliente), y que el momento que aporta la tensión es positivo (saliente), haciendo así que el momento nunca sea 0.
Dejo el diagrama de fuerzas del ejercicio, cuando me paro desde CM, se ve que ambas fuerzas generan momento para el mismo lado.
Cuando planteo desde el CM (a una distancia l de la recta AB), obtengo que el momento que aporta la normal es positivo (saliente), y que el momento que aporta la tensión es positivo (saliente), haciendo así que el momento nunca sea 0.
Dejo el diagrama de fuerzas del ejercicio, cuando me paro desde CM, se ve que ambas fuerzas generan momento para el mismo lado.
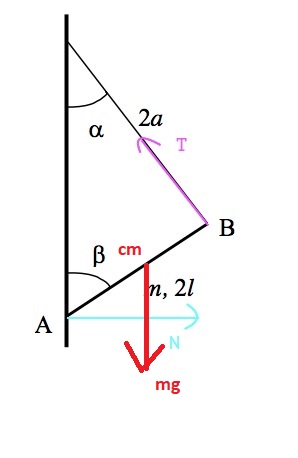
Perdón por la insistencia, pero no me cierra por qué me queda mal el momento visto desde CM, o desde B.
Gracias, saludos!
Estimado:
Ahora entendí tu duda. En efecto ambos momentos son positivos si A está por debajo del centro de masas. Pero si A está por encima del centro de masas el momento de la normal cambia de signo. El problema es que la posición de equilibrio no es para beta entre 0 y π/2 como está dibujado en la figura del ejercicio (no puede haber equilibrio en esta región), sino que beta tiene que ser mayor que π/2 (la barra, como el hilo también va hacia arriba desde B).
Ahora entendí tu duda. En efecto ambos momentos son positivos si A está por debajo del centro de masas. Pero si A está por encima del centro de masas el momento de la normal cambia de signo. El problema es que la posición de equilibrio no es para beta entre 0 y π/2 como está dibujado en la figura del ejercicio (no puede haber equilibrio en esta región), sino que beta tiene que ser mayor que π/2 (la barra, como el hilo también va hacia arriba desde B).
O sea, hay dos valores posibles de beta que verifican la relación 2lsen(beta)=2asen(alpha), uno mayor que π/2 y otro menor que π/2. El que sirve es el que es mayor que π/2.
Esto me hace pensar que también hay dos posibles valores de alpha que verifican la condición de equilibrio: uno menor que π/2 y otro mayor que π/2. ¿Puede ser alpha mayor que π/2?
Saludos:
Ricardo.
Buenas, ahora si me quedó claro, no me había dado cuenta que el beta del dibujo no estaba entre los valores posibles para el equilibrio.
Gracias por la pronta respuesta.
Gracias por la pronta respuesta.
Buenas, no entiendo el final del procedimiento. Yo llego a la condición de equilibrio, y luego me faltaría hallar los ángulos alfa y beta en función de los parámetros del problema (l y a). Llegué a esta fórmula: 2tan(alpha)=-tan(beta) y con trigonometría saqué el sen de alfa y el cos de alfa, y sabiendo que sen sobre cos es tan, llego a beta=arc tg (-2l/a). (luego hallo alfa). Por qué esto estaría mal? Por qué no parar ahí en vez de seguir hallando el arcsen?
En respuesta a Andrea Debora Pachalian Marashlian
Re: Ejercicio 4 y 5
Hola Andrea,
No entiendo cómo hallas el ángulo alfa solo con trigonometría, ni de donde sale la relación que mancionás sobre las tangentes.
La relación entre ángulos que podés sacar de la geometría es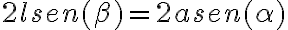 .
.
Luego tenés que hallar el de equilibrio con la ecuación de la energía.
de equilibrio con la ecuación de la energía.
En cualquier caso, subí una captura de tu desarrollo y me fijo si es correcto.
Saludos!
No entiendo cómo hallas el ángulo alfa solo con trigonometría, ni de donde sale la relación que mancionás sobre las tangentes.
La relación entre ángulos que podés sacar de la geometría es
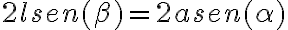 .
.Luego tenés que hallar el
 de equilibrio con la ecuación de la energía.
de equilibrio con la ecuación de la energía.En cualquier caso, subí una captura de tu desarrollo y me fijo si es correcto.
Saludos!
