Buenas, no pude llegar al resultado del 12 a), halle tetha en función del ángulo phi y sustituí como se muestra aquí abajo . Agradezco su me pueden dar una mano. Saludos
Hola,
Por lo que veo el error está en la relación entre alpha y phi. La relación que tenés es incorrecta. La geometría es la siguiente. La recta AB y la recta tangente a la circunferencia que A traza en el plano están contenidas en un plano vertical. Esto se debe a que ambas son perpendiculares a la recta OA, que está contenida en el plano horizontal. Esto implica necesariamente que la recta tangente a la cfa en A corta el eje j precisamente en la proyección de B en dicho eje. Es decir, si llamamos B' a esta proyección, sucede que el triángulo OB'A es rectángulo en A. Esto nos permite escribir el largo de OB' en términos de phi y el largo de OA, que es dato. Por otro lado, el largo de OB' se puede escribir también en términos de el largo de OB y alpha. Esto lleva de inmediato a una relación entre phi y alpha. De ahí se obtiene la solución derivando y operando.
Espero que esto te sirva, de lo contrario no dudes en volver a consultar.
Saludos
Guzmán
Profe, yo la verdad no me doy cuenta si me quedó bien, podrías escribir la solución o algo para poder comparar?
En términos de la notación del compañero, usando el razonamiento que escribí antes tenés

la velocidad de B es así que hay que hallar
así que hay que hallar  para resolver el ejercicio. Derivando la ecuación anterior de los dos lados tenes
para resolver el ejercicio. Derivando la ecuación anterior de los dos lados tenes

de donde se despeja . El problema es que de ahí nos queda
. El problema es que de ahí nos queda  en términos de
en términos de  . Pero
. Pero  se puede hallar usando que
se puede hallar usando que

para ángulos menores que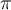 y la primer ecuación que escribí. De ahí operando se llega a la solución que aparece al final de la hoja de practico.
y la primer ecuación que escribí. De ahí operando se llega a la solución que aparece al final de la hoja de practico.

la velocidad de B es
 así que hay que hallar
así que hay que hallar  para resolver el ejercicio. Derivando la ecuación anterior de los dos lados tenes
para resolver el ejercicio. Derivando la ecuación anterior de los dos lados tenes
de donde se despeja
 . El problema es que de ahí nos queda
. El problema es que de ahí nos queda  en términos de
en términos de  . Pero
. Pero  se puede hallar usando que
se puede hallar usando que 
para ángulos menores que
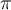 y la primer ecuación que escribí. De ahí operando se llega a la solución que aparece al final de la hoja de practico.
y la primer ecuación que escribí. De ahí operando se llega a la solución que aparece al final de la hoja de practico. Muchas gracias por tu respuesta Guzman, quedó claro y se pudo llegar al resultado. Saludos