Hola, quería consultar si me pueden explicar la respuesta del ejercicio 3 parte A /examen Julio 2021, porque no logro entender como el radio de convergencia es mas grande que R, siendo D(Zo,R) el disco donde esta definida f(z) y es holomorfa en ella. Adjunta las capturas del ejercicio. Gracias.
mmm, tal vez este ejemplo sea un poco clarificador:
 tal que
tal que  . El desarrollo en series de potencia de
. El desarrollo en series de potencia de  en
en 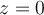 es
es  . El radio de convergencia es infinito! a pesar de que la función está definida solo en el disco de centro cero y radio 1.
. El radio de convergencia es infinito! a pesar de que la función está definida solo en el disco de centro cero y radio 1.
Entonces en realidad lo que sucede es que si bien está definida solo en un disco, si el radio de convergencia es más grande es porque
está definida solo en un disco, si el radio de convergencia es más grande es porque  se puede extender, o sea, definir en un conjunto un poco más grande.
se puede extender, o sea, definir en un conjunto un poco más grande.
Aclara un poco?
De la demostración que dan no sé si tenes alguna duda?
 tal que
tal que  . El desarrollo en series de potencia de
. El desarrollo en series de potencia de  en
en 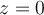 es
es  . El radio de convergencia es infinito! a pesar de que la función está definida solo en el disco de centro cero y radio 1.
. El radio de convergencia es infinito! a pesar de que la función está definida solo en el disco de centro cero y radio 1.Entonces en realidad lo que sucede es que si bien
 está definida solo en un disco, si el radio de convergencia es más grande es porque
está definida solo en un disco, si el radio de convergencia es más grande es porque  se puede extender, o sea, definir en un conjunto un poco más grande.
se puede extender, o sea, definir en un conjunto un poco más grande.Aclara un poco?
De la demostración que dan no sé si tenes alguna duda?
Se entendió el ejemplo, no sé si te animas a explicar la demostración, porque me cuesta ver como el radio de convergencia es mayor a R. Gracias.
Se entendió, gracias


![1/R = \limsup \sqrt[n]{\lvert a_n \rvert} \leq \limsup\sqrt[n]{M(R')/R'^n} = 1/R' 1/R = \limsup \sqrt[n]{\lvert a_n \rvert} \leq \limsup\sqrt[n]{M(R')/R'^n} = 1/R'](https://eva.fing.edu.uy/filter/tex/pix.php/ca9e413b17ccf4138ee0c8aec6292caa.png)
