CDIV-1S: Ejercicio de Múltiple Opción de Parcial 2019 Primer Semestre | FING

Página Principal

Ejercicio de Múltiple Opción de Parcial 2019 Primer Semestre

Buenas, el ejercicio me esta dando la opción B, cuando según las soluciones es A, y no encuentro el error.
De hecho, si ingreso la función a GeoGebra, y pido que me calcule la integral, me da la opción B.

Para resolverlo me fijé que

$\int_{0} ^ {x} t ^ 2 \, d t$ =

$\frac {x ˆ 3}{3}$ y que

$\int_{0} ^ {x} -2t + 4 \, d t$ =

$-x ^ 2$ +

$4x$ .
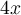Luego le calcule la imagen en 1 a las dos funciones para saber si era igual o no, y así dirimir entre la opción A y la B, que eran las que tenían dibujadas la función

$x ^ 3$ y

$-x ^ 2$ +

$4x$ .
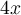En resumen una imagen es

$\frac {1}{3}$ y la otra es

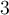$3$ , así que la función no debería ser continua como en la opción A.

Re: Ejercicio de Múltiple Opción de Parcial 2019 Primer Semestre

de Joaquin Vila David Lima - viernes, 6 de mayo de 2022, 13:43

Para -2t+4 tenés que integrar de 1 a x y sumarle la integral de 1 a 0 de t²

Re: Ejercicio de Múltiple Opción de Parcial 2019 Primer Semestre

de Sofia Llavayol Alvariño - viernes, 6 de mayo de 2022, 17:47

Lo que dice Joaquín está bien.
Te queda

$F(x)= \int_0^x t^2dt= x^3/3$ si

$x\in [0,1]$ y

$F(x)= \int_0^1 t^2 dt +\int_1^x (-2t+4) dt= (1/3)+\int_1^x (-2t+4) dt$ si

$x\in [1,2]$ .