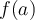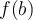Hola tengo una duda de este parcial en un verdadero y falso, no se si este es el foro adecuado pero no encontré uno para pruebas anteriores, la duda es sobre este ej:
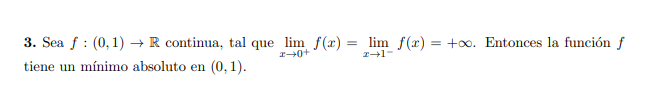
y tengo el siguiente contra ejemplo para decir que es falsa ya que no hay 1 mínimo absoluto sino que hay infinitos, en la imagen muestro 2:

pero sin embargo la afirmación es verdadera, no se en que me estoy equivocando.