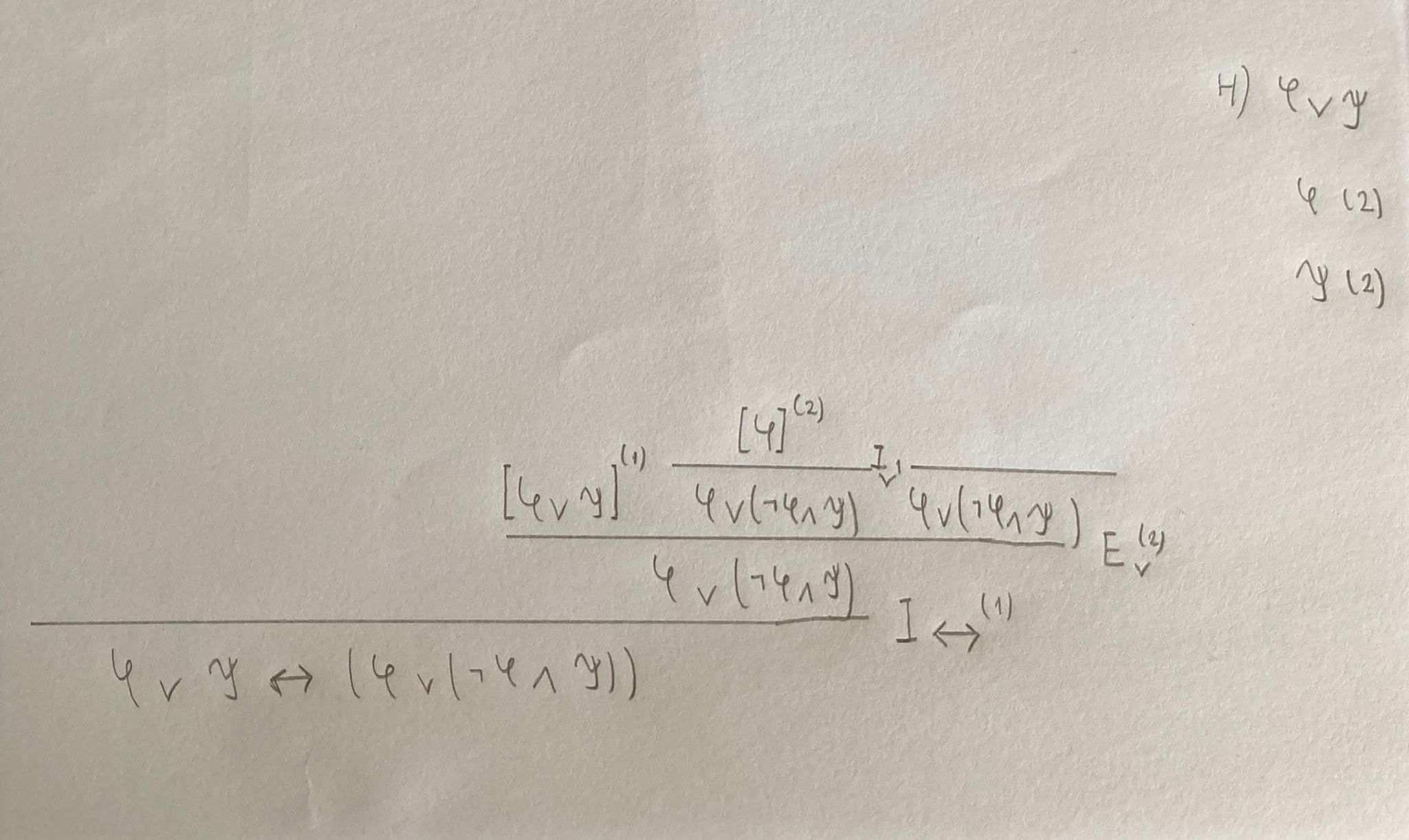Buenas, qué tal?
Algún pique para hacer este ejercicio?
Revisé el foro y los comentarios no me han servido, adjunto imagen de la letra y de lo que tengo hecho.
Gracias y saludos.
PD: La sub-rama izquierda la pude resolver utilizando la eliminación del OR aunque no se encuentre en la foto.
Hola:
Entiendo que te falta esta parte: ψ ⊢ φ ∨ (¬φ ∧ ψ)
Se puede construir con una aplicación de RAA:
[¬(φ ∨ (¬φ ∧ ψ)) ]¹ ψ
⋮
⋮
⊥
----------------- RAA¹
(φ ∨ (¬φ ∧ ψ))
La derivación anterior se puede construir con la siguiente estrategia:
1) Construir una derivación:
¬φ , ψ
⋮
(D₁)
⋮
(φ ∨ (¬φ ∧ ψ))
2) Construir una derivación:
φ , ψ
⋮
(D₂)
⋮
(φ ∨ (¬φ ∧ ψ))
Es decir, en un caso admitimos ¬φ como hipótesis y en el otro caso tomamos φ. En ambos casos, usamos eventualemente la hipótesis global ψ.
Una vez que tenemos ambas derivaciones, podemos armar la derivación buscada:
[φ]² , ψ
⋮
(D₂)
⋮
[¬ (φ ∨ (¬φ ∧ ψ))]¹ (φ ∨ (¬φ ∧ ψ))
--------------------------------- E¬
⊥
------------------- I¬²
¬φ
⋮
(D₁)
⋮
[¬ (φ ∨ (¬φ ∧ ψ))]¹ (φ ∨ (¬φ ∧ ψ))
--------------------------------------- E¬
⊥
------------------ RAA¹
(φ ∨ (¬φ ∧ ψ))