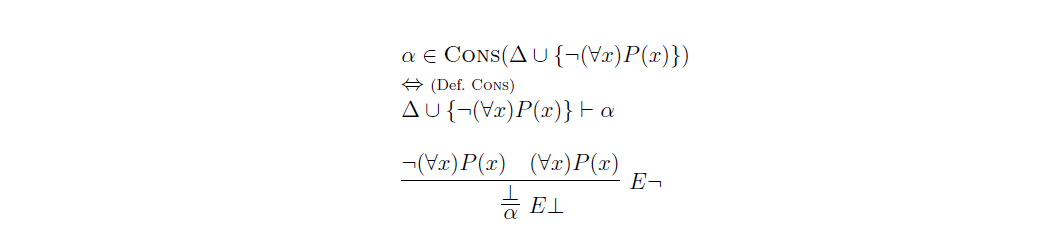Buenas, no entiendo como deduce en la segunda parte que Alfa pertenece a Delta u Phi, ya que las hipótesis de la derivación son, el Phi que nos tomamos y uno de los dos elementos del Delta dado.
No debería tener también al otro elemento de Delta en las hipótesis de la derivación?
Saludos y gracias.
Michel!