Foro Práctico I

Hola, Martina. No está del todo mal tu planteo, pero hay que resolver una confusión al aplicar los teoremas de Roberval y Coriolis.

El sistema que estás considerando como móvil es tal que la posición del punto P queda fija, siempre en $\vec r'_P = r \hat e_r$. Este sistema móvil gira de tal manera que siempre "ve" al punto P en el mismo sitio. Por esa razón, tanto la velocidad como la aceleración relativas de P son cero en este sistema móvil.

En el cálculo de la velocidad relativa derivando la posición relativa, hay que considerar la base móvil constante:

$\vec v ' = \dfrac{d' \vec r'}{dt} = \dfrac {d' (R \hat e_r)}{dt}=0$

En tu planteo sumaste una velocidad relativa y una aceleración relativa que no son cero. De hecho, sumaste los valores correspondientes a los valores vistos en tu sistema absoluto. Eso explica por qué obtuviste el doble del resultado correcto.

-----

Hay un sistema de referencia adicional en este ejercicio, cuya base no aparece dibujada: un sistema fijo en el cual la barra OA aparece rotando con velocidad angular de módulo 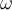$\omega$. 

A mi entender, en este ejercicio ESE es el sistema que considera absoluto, y los dos sistemas que tú planteaste son móviles. Para llegar a las mismas respuestas publicadas en la solución, hay que considerarlo de esa manera. Sin embargo, el enunciado es algo ambiguo, y estrictamente hablando, se trata de un asunto de interpretación.

Normalmente, para cada objeto es preferible tener un único sistema móvil. Usando como sistema fijo el que yo mencioné antes, ¿se te ocurre cómo combinar los dos sistemas que tú planteaste para obtener un sólo sistema móvil? ¿En qué cambian el planteo y los cálculos?

------

Saludos,
NC