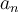FVC-1S: Ejercicio 3

Buenas, estaba realizando el ejercicio 3. Para realizarlo se me ocurrió hallar la serie de potencia para luego usar la definición de radio de convergencia y llegar al resultado. Haciendo esto logré hallar la serie $\sum{n=1, \infty } ( \frac{z^{2n-1}}{2^{2n-1}}+ \frac{z^{2n}}{2^{2n-2}} )$

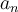No logro despejar $z^n$ para obtener $a_n$ y calcular el radio de convergencia.

Como puedo seguir?

Re: Ejercicio 3

de Alejandro Bellati - miércoles, 23 de marzo de 2022, 10:38

No estoy seguro a qué te referís con hallar la serie de potencia. Los coeficientes

$a_n$ ya están dados,

$a_1 = 1/2, a_2 = 1, a_3 = 1/8, a_4 = 1/4, a_5 = 1/32, a_6 = 1/16, a_7 = 1/128, a_8 = 1/64 ...$

Si querés escribir una fórmula podes escribir algo así :

$a_n = \frac{1}{2^n}$ si

$n$ es impar y

$a_n = \frac{1}{2^{n-2}}$ si

$n$ es par.

Saludos