¿Alguien pudo resolver el ejercicio 20?

No encuentro un camino claro para encarar la resolución
Gracias por la ayuda
Javier

 y consideras dos bases
y consideras dos bases 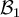 y
y 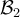 de
de  , las matrices
, las matrices  y
y  siempre son semejantes (ver teórico). Entonces, se cumple la igualdad que dices y en particular existen esas matrices de cambio de bases, donde una es la inversa de la otra. El propósito del ejercicio 20 es ver si es posible que exista
siempre son semejantes (ver teórico). Entonces, se cumple la igualdad que dices y en particular existen esas matrices de cambio de bases, donde una es la inversa de la otra. El propósito del ejercicio 20 es ver si es posible que exista 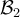 tal que
tal que  sea la matriz que se dice en la letra. Te recomiendo que supongas que sí y que luego uses las propiedades de la semejanza de matrices para ver qué se puede concluir.
sea la matriz que se dice en la letra. Te recomiendo que supongas que sí y que luego uses las propiedades de la semejanza de matrices para ver qué se puede concluir. Gracias!