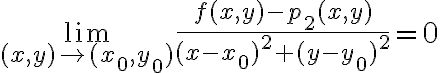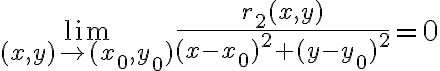Hola. La idea es usar el teorema de Taylor. Si 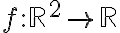 es de clase
es de clase 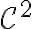 (es decir, si existen todas las derivadas parciales de
(es decir, si existen todas las derivadas parciales de  hasta orcen 2 y son continuas) y le llamo
hasta orcen 2 y son continuas) y le llamo 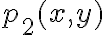 al polinomio de orden 2 de
al polinomio de orden 2 de  en un punto
en un punto 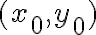 , entonces el teorema de Taylor nos dice que:
, entonces el teorema de Taylor nos dice que:
En general el teorema se enuncia llamándole resto (de orden 2 en este caso) a la función 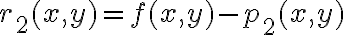 y se escribe como:
y se escribe como:
Entonces, en el ejercicio tenemos una función 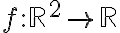 definida como
definida como 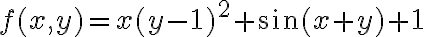 y queremos ver qué polinomio de grado 2 tenemos que restarle a
y queremos ver qué polinomio de grado 2 tenemos que restarle a  para que el límite de
para que el límite de  menos ese polinomio dividido
menos ese polinomio dividido 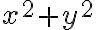 sea 0. El teorema de Taylor nos asegura que el único polinomio que cumple eso es el de Taylor (es decir, el polinomio que tiene que aparecer restando para que ese límite sea 0 tiene que ser el polinomio de Taylor). Para resolver el ejercicio entonces basta con calcular el polinomio de Taylor de orden 2 de
sea 0. El teorema de Taylor nos asegura que el único polinomio que cumple eso es el de Taylor (es decir, el polinomio que tiene que aparecer restando para que ese límite sea 0 tiene que ser el polinomio de Taylor). Para resolver el ejercicio entonces basta con calcular el polinomio de Taylor de orden 2 de  en
en  y sumar sus coeficientes.
y sumar sus coeficientes.
Saludos